트리(Tree) 란?
수학, 그래프 이론에서는 회로가 없는 무방향의 그래프를 트리라고 정의합니다. 이는 자료구조에서 쓰이는 트리와 기본적으로 같지만 차이가 좀 있습니다. 무슨 말인지 쉽게 알아봅시다.
트리는 스택이나 큐 같은 선형 자료 구조가 아닌 노드로 이루어진 비선형 자료구조입니다. 트리는 계층 간의 관계를 표현하는 자료구조입니다. 트리는 아래의 특징들을 가집니다.
1. 트리는 하나의 루트 노드를 가진다.
2. 루트 노드는 0개 이상의 자식 노드를 가진다.
3. 자식 노드 또한 0개 이상의 자식 노드를 가진다.
4. 노드와 노드들을 연결하는 간선(Edge) 들로 구성되어 있다.
5. 트리에는 사이클(cycle) 이 존재할 수 없다. 사이클이란 시작 노드에서 출발해 다시 시작 노드로 돌아올 수 있는 경로가 있다면 사이클이 존재한다고 한다.
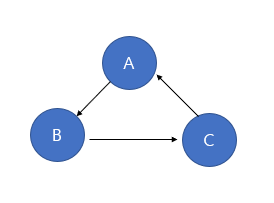
트리는 사이클이 없는 하나의 연결 그래프(Connected Graph) 라고 할 수 있습니다. 또한 트리의 노드는 self-loop 가 존재 하면 안됩니다.
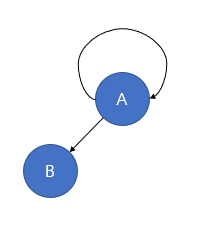
이러한 특성으로 유추를 해보면, N개의 노드를 가지는 트리는 항상 N-1 개의 간선(edge) 를 가집니다. 각 노드들마다 무조건 연결이 되어있어야 하고, 자기 자신과 연결되지 않고, 사이클이 없기 때문에 중복해서 연결되는 경우도 없기 때문입니다. 그리고 모든 자식 노드는 한 개의 부모 노드만을 가지는 형태로 구성됩니다.
트리 관련 용어

- 루트 노드(root node) : 부모가 없는 노드로 트리는 단 하나의 루트 노드를 가집니다.
- 단말 노드(leaf node) : 자식이 없는 노드로 terminal 노드라고도 부릅니다. ( C, D, E )
- 내부 노드(internal nde) : 단말 노드가 아닌 노드 ( A, B )
- 간선(edge) : 노드를 연결하는 선
- 형제(sibling) : 같은 부모 노드를 가지는 노드들 ( B-C , D-F )
- 노드의 깊이(depth) : 루트 노드에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- 노드의 레벨(level) : 트리의 특정 깊이를 가지는 노드의 집합 ( ex : Level 1 {B, C}, Level 2 {D, E} )
- 노드의 차수(degree) : 자식 노드의 개수
- 트리의 차수(degree of tree) : 트리의 최대 차수
트리의 종류
이진 트리 (Binary Tree)
이진트리는 각 노드가 최대 두 개의 자식을 가지는 트리를 뜻합니다. 각 노드는 자식이 없거나 한 개이거나 두 개만을 갖는 구조의 트리를 모두 이진 트리라고 합니다.
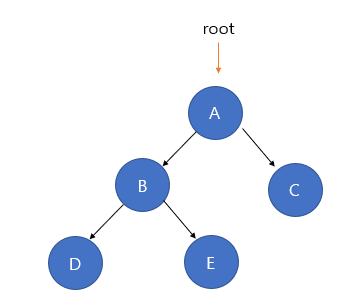
이진 트리는 탐색을 할 때 유용하게 사용되는 구조입니다. 이진트리의 탐색에는 전위 순회, 중위 순회, 후위 순회 방법이 있는데 이는 다음 포스팅에서 다뤄보도록 하겠습니다.
완전 이진 트리 (Complete Binary Tree)
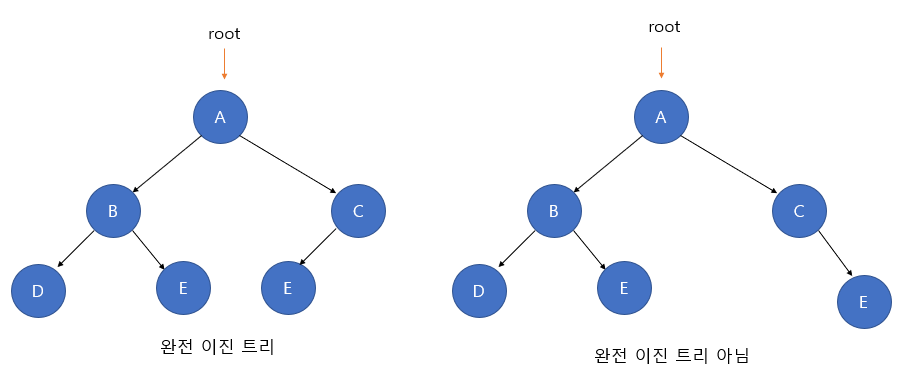
완전 이진트리는 이진트리 + 특정 조건 이라고 생각하시면 됩니다. 완전 이진트리는 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있어야 합니다. 즉 위쪽부터 차곡차곡 데이터가 쌓이면서 내려가야한다는 말이죠.
그리고 마지막 레벨은 꽉 차 있지 않아도 되지만, 노드가 왼쪽에서 오른쪽으로 채워져야 합니다.
위의 조건을 만족하는 완전이진트리는 마지막 레벨을 h 라고 하면 1 ~ 2h - 1 개의 노드를 가집니다.
완전 이진 트리는 데이터가 빠짐없이 채워져있기 때문에 배열을 사용해 효율적으로 표현할 수 있습니다.
왜 배열로 표현이 쉬운가? 는 좀 더 아래에서 알아볼 포화 이진트리에서 다시 설명하도록 하겠습니다.
전 이진 트리 (Full Binary Tree)

전 이진트리는 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리입니다. 자식 노드가 1개인 경우는 전 이진 트리가 아닙니다.
포화 이진 트리 (Perfect Binary Tree)
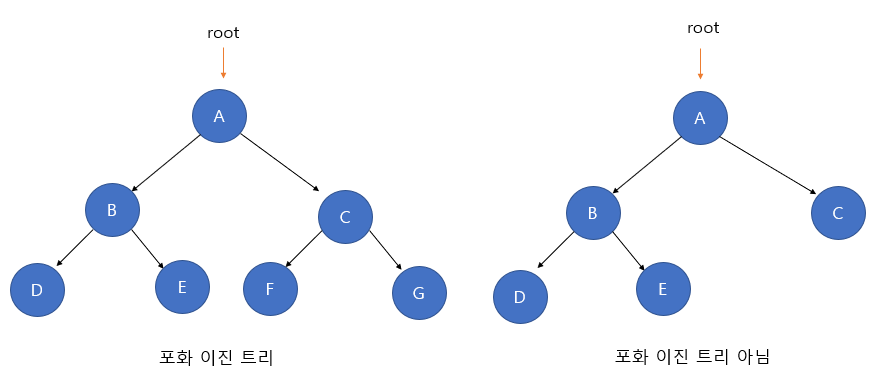
포화 이진트리는 모든 레벨이 노드로 꽉 차 있는 트리를 뜻합니다. 포화 이진 트리는 모든 말단 노드가 동일한 깊이 도는 레벨을 가집니다. 포화 이진트리의 경우 트리의 높이를 k 라고 하면 노드의 개수가 정확히 2^k - 1 개 입니다.
포화 이진트리는 완전 이진 트리의 상위호환? 이라고 해야할까요, 포화 이진트리와 완전 이진트리는 배열로 나타내면 노드 번호가 일치한다는 특성이 있습니다. 포화 이진 트리는 배열로 표현하기가 굉장히 쉽습니다. 그 이유는 부모 노드와 자식 노드의 관계가 유지되기 때문입니다.

지금 노드의 번호를 따라가다보면 자식 노드는 규칙이 있습니다. 부모의 인덱스를 k 라고 하면 왼쪽 자식 노드의 인덱스는 2k, 오른쪽 자식 노드의 인덱스는 2k+1 이 됩니다. 포화 이진 트리나 완전 이진트리가 배열을 통해 구현하는 것이 효율적인 이유는 다음과 같습니다.

부모 노드와 자식 노드의 인덱스 관계
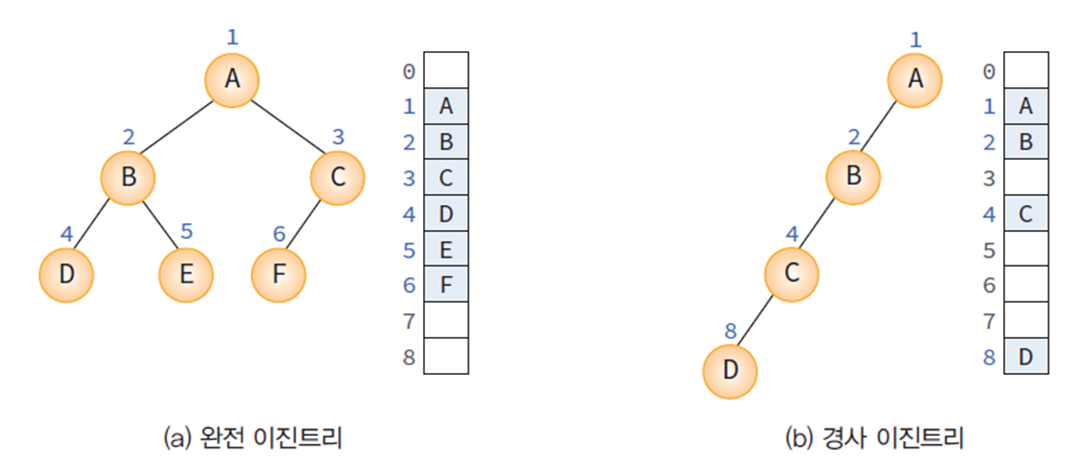
이것이 완전 이진 트리가 배열로 구현하면 효율적인 이유입니다.
이진 탐색 트리 (Binary Search Tree)

이진 탐색 트리는 이진트리이면서 아래와 같은 속성을 가지는 트리를 말합니다.
- 이진 탐색 노드의 저장된 키(key) 는 유일하다.
- 부모의 키가 왼쪽 자식 노드의 키보다 크다.
- 부모의 키가 오른쪽 자식 노드의 키보다 작다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
이러한 이진 탐색 트리는 효율적인 탐색을 위해 고안된 트리입니다. 이진 탐색 트리를 이용한 정렬 알고리즘을 사용하면 선택 정렬이나 삽입 정렬 같은 방법보다 훨씬 낮은 시간복잡도로 정렬이나 탐색이 가능합니다. 이는 다른 포스팅에서 제대로 다뤄볼 예정입니다.
[C 자료구조] 이진 탐색 트리 (Binary Search Tree)
이진 탐색 트리(Binary Search Tree) [C 자료구조] 트리(Tree) 의 종류 트리(Tree) 란? 수학, 그래프 이론에서는 회로가 없는 무방향의 그래프를 트리라고 정의합니다. 이는 자료구조에서 쓰이는 트리와 기
songsite123.tistory.com
여기까지 트리의 개념과 용어 정리, 종류에 대해 간략히 알아보았습니다. 감사합니다.

참고 및 출처 :
https://code-lab1.tistory.com/8
C언어로 쉽게 풀어쓴 자료구조 - 생능출판
'C 자료구조' 카테고리의 다른 글
| [C 자료구조] 스택을 이용한 트리 순회 (전위/중위/후위) (0) | 2023.05.25 |
|---|---|
| [C 자료구조 ] 트리의 순회(Traversal of Tree) - 전위 / 중위 / 후위 (1) | 2023.05.25 |
| [C 자료구조] 그래프 ADT 구현 : 인접행렬 / 인접리스트 (2) | 2023.05.25 |
| [C 자료구조] 그래프(Graph)의 종류 : 인접 행렬(Adjacent matrix) vs 인접 리스트(Adjacent list) (0) | 2023.05.24 |
| [C 자료구조] 큐(Queue) - 연결리스트 구현 (0) | 2023.05.24 |