[ISL] Linear Regression (선형 회귀)

 

 

[목차]

• Introduction

• Simple Linear Regression

• Estimating the Coefficients

• Accuracy of the Coefficients Estimates

• Significance of the Model

• Overall Accuracy of the model

• Multiple Linear Regression

• Some Important Questions

• Potential Problems

• Comparision of Linear Regression with K-Nearest Neighbors

---

 Introduction

 

[ISL] Statistical Learning ( 통계적 학습 )

지난 단원에서 Statistical Learning 이란 무엇인지, 그 중에서도 예시로 지도학습, 그 중에서도 regression 을 사용해서 설명했습니다. 이번 단원은 regression 에 대해 자세히 알아보는 단원입니다.

 

Linear regression 는 가장 간단한 형태의 supervised learning 으로 quantitative response 에 대한 예측에 효과적입니다.

 

간단하기 때문에 다른 복잡한 statistical learning 방법에 비해 안 좋아보일 수 있지만 실제로 많이 사용되고 있으며 이후 더 복잡한 모델을 이해하는데 도움이 되기 때문에 여기서부터 잘 이해하는 것이 중요합니다. 또한 후에 배울 여러가지 복잡한 방법들로 충분히 선형 회귀 모델로 일반화 혹은 확장이 가능합니다.

 

 

 

 Simple Linear Regression

 

임의의 변수 $X$ 와 $Y$ 간 관계를 알아보고 싶을 때 먼저 산점도 등으로 데이터의 분포를 시각화해서 확인하는 것이 필요합니다. 왜냐하면 같은 모델이 나오는 데이터여도 실제 분포나 그래프가 매우 다르게 나타날 수 있기 때문입니다. 

앤스컴 콰르텟 - 위키백과, 우리 모두의 백과사전

 

만약 선형 관계가 있을 것이라 생각하면 간단한 Simple linear regression 식을 세울 수 있습니다.

 

$$ Y \approx \beta_0 + \beta_1 X $$

 

실제로는 error term $\epsilon_i$ 가 존재하기 때문에 = 가 $\approx $ 로 나타나죠. 완벽한 선형관계가 아니라면 등호는 성립하지 않는데 실제로 그럴 일은 없다고 보시면 됩니다. 또한 Y가 X 이외의 다른 요소에도 영향을 받게 되면 그 부분 또한 ε 으로 나타납니다. 선형 회귀 모델에서의 목적은 가장 그럴싸한 $\beta_0, \ \beta_1$ 값들을 찾아내는 것이고 이를 바탕으로 $x$가 주어지면 $y$를 예측할 수 있습니다. 앞에서도 추정치는 hat 을 사용해 표현했으므로

 

$$ \hat{y} = \hat{\beta _0 } + \hat{ \beta_1} x $$

 

위의 식으로 나타낼 수 있습니다.

 

Simple linear regression 에서 Simple 은 predictor 가 1개라는 뜻이고 여러 개 있는 경우는 Multiple 이라고 합니다. 또한 linear 는 predictor 가 선형이라는 것이 아니라 파라미터$\beta$들이 선형적으로 연결되어 있음을 의미합니다. 이 말은 곧 데이터의 분포가 선형이 아니더라도 linear regression 으로 표현할 수 있으며 차후에 이 내용을 기반으로 non-linear relationship 을 linear regression 으로 fitting 합니다.

 

 

 Estimating the Coefficients

 

$\beta_0$와 $\beta_1$ 을 찾는 방법은 여러가지가 있지만 가장 흔하게 사용되는 방법은 least squares method, 최소제곱법 입니다.

최소제곱법 - 위키백과, 우리 모두의 백과사전

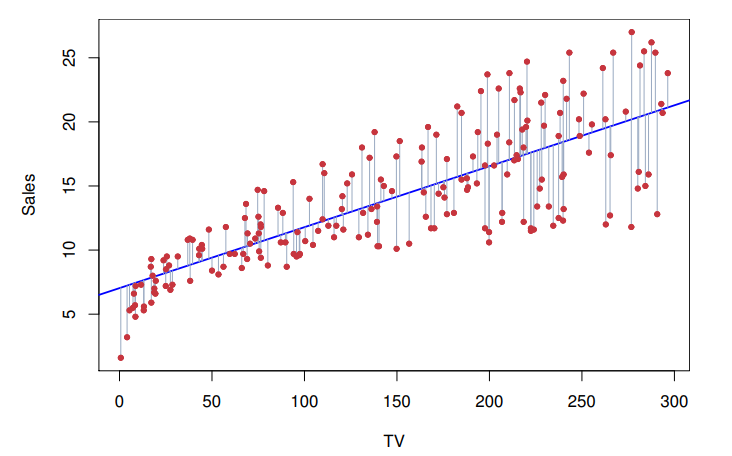
Linear regression model 에서 오차는 빨간 점과 파란 선 사이의 거리입니다. 앞에서 이를 residual 라 부른다고 배웠죠.

 

이를 수식적으로 나타내면

 

$$ \hat{y_i} = \hat{ \beta _0} + \hat{ \beta_1} x_i $$

$$ e_i = y_i - \hat{y_i} $$

 

$e_i$ 를 $i$ 번째 residual 라고 하며 주어진 데이터가 $n$개라면 $n$개의 residual 이 존재합니다. 여기서 Residual Sum of Squares (RSS) 라는 것을 정의하는데 이름 그대로 residual 제곱들의 합입니다.

 

$$ \text{RSS} = e_1^2 + e_2^2 + \cdots + e_n^2 $$

 

위 식에서 e의 정의대로 넣고 파라미터 $\beta$ 에 대해 정리를 해보면

 

 

$$  \text{RSS} = \sum _{i=1}^n e_i^2 = \sum_ {i=1}^n (y_i - \hat{y_i}) = \sum_ {i=1}^n (y_i - \hat{\beta _0} - \hat{\beta _1} x_i )^2$$

 

 

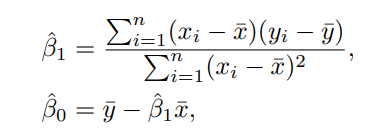
이 때 갑자기 $\overline{x}$랑 $\overline{y}$ 가 튀어나와서 당황스러우실 수 있는데 이는 그냥 sample, 즉 $ \overline {x} = \dfrac{1}{n} \sum_{i=1}^n x_i \quad , \quad \overline{y} = \dfrac{1}{n} \sum_{i=1}^n y_i $를 의미합니다.

 

RSS(Residual Sum of Square) 함수는 2개의 파라미터로 구성된 다변수 함수 이기 때문에 다변수 함수에 적용되는 라그랑즈 승수법에 의해 ($x_i$, $y_i$는 주어진 데이터이므로 상수) gradient 를 영벡터로 만드는 값이 곧 $\beta_0$, $\beta_1$의 추정치가 되며 자세한 증명은 아래 링크를 참고해주시면 됩니다.

Lagrange multiplier - Wikipedia

 

 

제곱을 하는 이유는 + 오차와 - 오차가 상쇄되는 것을 방지하기 위함인데, 이런 이유 때문에 제곱을 하는 것이라면 $| e_i | $ 를 사용해도 무방합니다. 이를 LAD(Least Absolute Deviations) 라고 하며 이는 이상치에 민감하지 않다는 장점이 있지만 추정치가 하나로 나오지 않고 계산이 어려워진다는 단점을 가지고 있습니다.

Least absolute deviations - Wikipedia

 

 

https://slideplayer.com/slide/13493423/

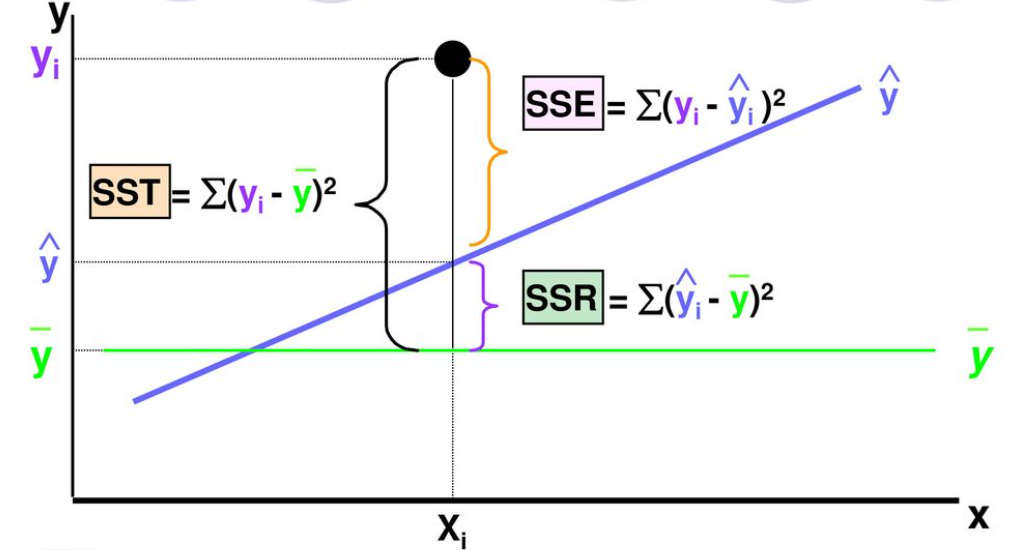
위 그림은 regression 식과 residual 을 시각적으로 표현한 그래프와, 옆에 그 수식이 나와 있는 그래프입니다. 위 그래프에서는 SST, SSE, SSR 이라는 용어를 사용하고 있지만 ISL 에서는 TSS(Total Sum of Squares), RSS(Residual Sum of Squares), ESS(Explained Sum of Squares) 라는 용어로 사용합니다.

 

그림으로만 봐도 TSS = RSS + ESS 인 것이 눈으로 보이는데요, 이는 간단한 조작을 통해 구할 수 있습니다.

$$ \begin{align*} & y_i = \bar{y} = (y_i - \hat{y}_i)+(\hat{y}_i - \bar{y}) \\ & \to (y_i - \bar{y})^2 = (y_i - \hat{y}_i)^2 + (\hat{y}_i - \bar{y})^2+2(y_i-\hat{y}_i)(\hat{y}_i-\bar{y})\\ & \to \sum_{i=1}^n (y_i - \bar{y})^2=\sum_{i=1}^n(y_i-\hat{y}_i)^2+\sum_{i=1}^n(\hat{y}_i-\bar{y})^2+\sum_{i=1}^n2(y_i-\hat{y}_i)(\hat{y}_i-\bar{y})\\ & \to \sum_{i=1}^n(y_i-\bar{y})^2=\sum_{i=1}^n(y_i-\hat{y}_i)^2+\sum_{i=1}^n(\hat{y}_i-\bar{y})\\ & \to TSS \quad \quad = \quad \quad  RSS \quad \quad  + \quad \quad ESS \end{align*} $$

 

완전제곱을 전개하면서 나오는 $2(y_i-\hat{y}_i)(\hat{y}_i-\bar{y})$ 부분은 0이 됩니다. 이는 $\sum e_i = 0$, $\sum x_ie_i = 0$ 임을 이용하면 증명할 수 있습니다.

 

 

위 식의 결론은, 총 편차의 제곱합(TSS)은 회귀식으로 설명되는 부분의 제곱합(ESS)와 설명되지 않는 부분의 제곱합(RSS)의 합으로 구성된다. 라는 것입니다. Lease Squared Method 가 RSS를 최소화 하는 estimator 를 찾는 것이기 때문에 결국 ESS가 커지는 estimator 를 찾는 것으로 생각할 수 있습니다.

 

 

TSS 는 n-1 의 자유도를 가지고 RSS 는 n-2 의 자유도, ESS 는 1의 자유도를 가집니다. $(n-1 = n-2 + 1)$

자유도를 논하기엔 저의 통계학적 지식이 아직 부족하기 때문에 자유도의 의미를 나타내는 블로그 글을 첨부합니다.

왜 표본(샘플)의 분산에서는 n이 아닌 n-1로 나눌까?

 

 

 Accuracy of the Coefficients Estimates

 

앞에서 구한 파라미터들의 추정치는 주어진 데이터를 바탕으로 구했기 때문에 데이터가 변하면 추정치 또한 변화합니다. 처음부터 구하고자 했던 $Y=\beta_0 + \beta_1 X + \epsilon $ 에서 $Y=\beta_0 + \beta_1 X$ 를 population regression line 이라고 하며, LSM 으로 구한 직선을 least squares line 라고 한다.

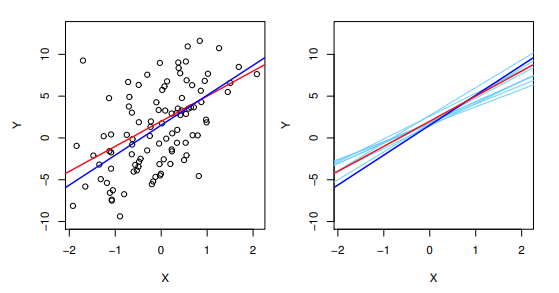
위 그래프에서 빨간 선은 population regression line 이고 (실제로 알 수 없지만 교재 내에서 그래프로 나타내기 위해 f(X) = 2 + 3X 로 가정하여 나타냄) 파란 선과 하늘색 선들은 데이터를 랜덤 샘플링할 때마다 구해지는 leaset squares line 입니다.

 

$ \beta_0$, $ \beta_1$ 을 추정하는 것은 통계에서 주어진 샘플을 바탕으로 모평균 같은 모집단의 특성을 추정하는 것과 유사합니다. 표본평균은 불편 추정량, unbiased estimator 이기 때문에 표본평균들의 평균은 모평균과 같습니다.

 

이와 마찬가지로 $ \beta_0 $, $ \beta_1 $ 의 추정치들도 많은 시행을 반복하여 평균을 구하면 실제 $ \beta_0 $, $ \beta_1 $ 과 같아집니다. 하늘색과 파란색 선들의 평균이 곧 빨간 색 선이 된다는 의미입니다.

( 증명 링크 : https://towardsdatascience.com/linear-regression-with-ols-unbiased-consistent-blue-best-efficient-estimator-359a859f757e ) 

 

 

 $ \beta_0 $, $ \beta_1 $ 의 추정치들의 평균이 실제  $ \beta_0 $, $ \beta_1 $ 와 같은데, 각 $ \beta_0 $, $ \beta_1 $의 추정치를 구하면 실제  $ \beta_0 $, $ \beta_1 $ 와는 얼마나 차이가 나지? 의 개념을 standard error 라고 합니다. 일반적으로 $ SE(\hat{\mu})$ 로 표기합니다. 

where σ^2 = Var(ε)

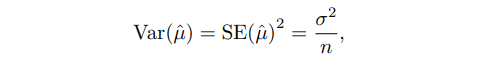
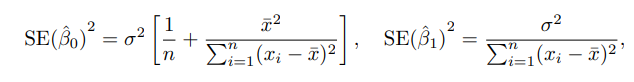
위 식을 해석해보면, 기울기의 추정치인 $ \hat{\beta_1}$ 는 $x_i$의 분산이 커질수록 분모가 커지기 때문에 값이 작아집니다. 즉 이는 데이터가 x축을 기준으로 넓게 퍼져있고 데이터의 개수가 많을 수록 기울기를 추정한  $ \hat{\beta_1}$ 이 실제 $ \beta_1 $에 더 가깝게 나온다는 의미를 가집니다.

 

따라서 만약 모든 데이터가 작은 구간에 몰려있는 경우, 그 데이터로 기울기를 추정하면 구할 때마다 기울기가 제멋대로 나올 가능성이 높고 변동성도 크게 나타나게 됩니다.

 

 

 Significance of the Model

 

 

 

 

 Overall Accuracy of the model

 

 

 

 

 Multiple Linear Regression

 

 

 

 

 Some Important Questions

 

 

 

 

 Potential Problems

 

 

 

 

 Comparision of Linear Regression with K-Nearest Neighbors