데이콘이란, 일종의 한국판 캐글로 데이터 분석과 여러 데이터를 머신러닝으로 다뤄보며 경진대회까지 참여할 수 있는 기회를 제공하는 사이트입니다. 외부교육을 듣다 처음으로 데이콘이라는 것에 대해 알고 참가하게 되었는데 아무것도 모른 채 참여할 수 없기 때문에 지난 대회에서 1등을 한 코드들을 분석해보고, 직접 colab으로도 이것저것 바꿔가며 돌려보는 포스팅입니다.
이번 포스팅에서 다루는 주제는 반도체의 박막 두께 분석 에 대한 내용입니다.
월간 데이콘 반도체 박막 두께 분석 경진대회 - DACON
분석시각화 대회 코드 공유 게시물은 내용 확인 후 좋아요(투표) 가능합니다.
dacon.io
위 사이트에서 데이터를 다운 받을 수 있습니다. 우승 코드는 포스팅 맨 하단의 주소에서 다운 가능합니다.
최근 고사양 반도체 수요가 많아지면서 반도체를 수직으로 적층하는 3차원 공정이 많이 연구되고 있습니다. 반도체 박막을 수십 ~ 수백 층 쌓아 올리는 공정에서는 박막의 결함으로 인한 두께와 균일도가 저하되는 문제가 있습니다. 이는 소자 구조의 변형을 야기하며 성능 하락의 주요 요인이 됩니다. 이를 사전에 방지하기 위해서는 박막의 두께를 빠르면서도 정확히 측정하는 것이 중요합니다. 박막의 두께를 측정하는 방법으로 반사율 측정이 널리 사용되며 반사율은 입사광 세기에 대한 반사광 세기의 비율로 정해집니다. (반사율 = 반사광/입사광) 반사율은 빛의 파장에 따라 변하며 파장에 따른 반사율의 분포를 반사율 스펙트럼이라고 합니다.
박막의 두께 측정을 위해 광스펙트럼 분석이 널리 사용되지만, 광 스펙트럼을 분석하기 위해서는 해당 분야의 전문가가 필요하며, 고성능의 컴퓨팅 성능이 요구됩니다. 따라서 이번 대회의 목적은 주어진 여러 개의 Layer로 구성된 반도체의 두께 및 반사율 스펙트럼 데이터를 통해 머신러닝을 하고, 그 모델을 사용해 스펙트럼 데이터만으로 두께를 예측하는 것입니다.
질화규소(layer_1)/이산화규소(layer_2)/질화규소(layer_3)/이산화규소(layer_4)/규소(기판) 총 5층 구조로 되어 있습니다. 대회의 목적은 기판인 규소를 제외한 layer_1 ~ layer_4의 두께를 예측하는 것으로 train.csv 파일에는 각 층의 두께와 반사율 스펙트럼이 포함되어 있습니다.
train.csv 파일에는 4층 박막의 두께와 파장에 따른 반사율 스펙트럼이 주어집니다. 헤더의 이름에 따라 layer_1 ~ 4는 해당 박막의 두께, 0~225은 빛의 파장에 해당하는 반사율이 됩니다. 헤더 이름인 0~225은 파장을 뜻하며 비식별화 처리가 되어있어 실제 값과는 다릅니다.
데이터 분석
우선 학습 데이터 전체를 볼 수는 없으니 데이터를 읽어오고 head() 함수를 사용해 일부분을 확인해보겠습니다.
import numpy as np
import pandas as pd
train = pd.read_csv('/content/drive/MyDrive/dacon/반도체 박막 두께 분석 경진대회_data/train.csv')
test = pd.read_csv('/content/drive/MyDrive/dacon/반도체 박막 두께 분석 경진대회_data/test.csv')
print("train shape is", train.shape)
print("test shape is", test.shape)
train.head()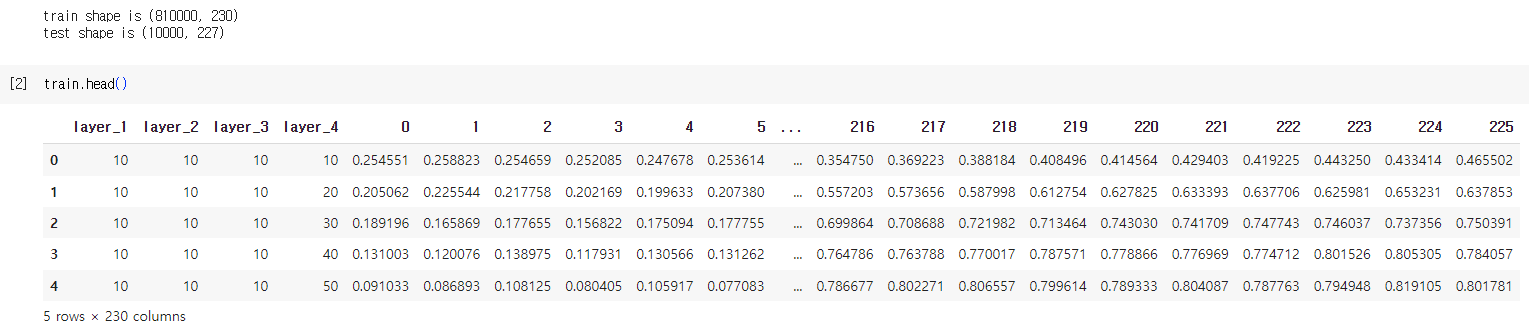
데이터의 첫 번째 열은 데이터의 순서를 나타냅니다. layer_1부터 layer_4 열까지는 각 박막의 두께, 그 이후부터는 파장 역수와 반사율 스펙트럼 등으로 구성되어 있습니다. 관찰된 자료를 이용해 각 박막 두께 간의 관계를 딥러닝 모델로 모형화하여 측정된 두께 데이터를 바탕으로 모델의 파라미터가 데이터를 잘 표현할 수 있게 학습한다면 새로운 데이터가 들어왔을 때도 두께를 예측할 수 있습니다. 즉 이 문제는 회귀 문제의 일종이며, 딥러닝 기반의 MLP로 시도해볼 수 있습니다.
train.shape 를 출력할 때 (810000, 230)되는 것을 확인할 수 있고 그 중 열을 나타내는 230은 226개의 반사율 스펙트럼과 각 층에 해당하는 박막 두께 정보 4개가 합쳐져서 230으로 나타납니다. 이런 데이터가 810000개 있다는 뜻이죠.
test.shape 는 (10000,226) 으로, 예측해야하는 박막 두께만 빠진 반사율 스펙트럼 데이터가 1만개 있는 겁니다.
train.info()
train.loc[:,'0':'225'].describe()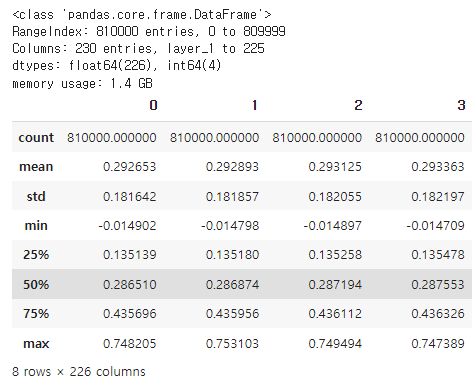
info() 를 통해 데이터 타입을 확인할 수 있습니다. dtypes 를 통해 학습 데이터가 float64형 변수 226개, int64형 변수 4개로 구성되어있음을 확인할 수 있습니다. 즉 박막 두께의 10 단위의 정수형은 int64형, 반사율 스펙트럼 데이터는 float64형 입니다.
다음으로 describe() 를 통해 기본적인 통계량을 확인할 수 있습니다. 이 때 loc 을 통해 0~225 열의 데이터로만 통계량을 측정합니다. 당연히 정답 데이터인 박막 두께 데이터는 빼고 통계를 확인해야겠죠?
눈에 띄는 점이라면 min 값이 대부분 음수라는 점입니다. 이게 어떤 데이터냐에 따라 음수값을 처리하는 방식이 달라지는데, 반사율은 음수 값이 나올 수 있고 데이콘 상에서 음수 데이터는 정상 데이터라고 명시해주었습니다. 또한 값 자체가 전부 1을 넘지 않으므로 따로 정규화를 진행하지 않더라도 대략 0~1 사이의 범위에 들어오는 데이터임을 확인할 수 있습니다.
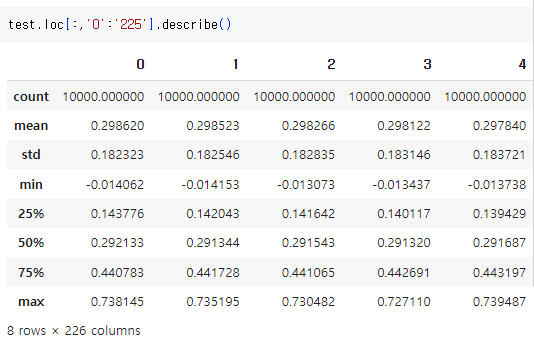
test 데이터의 기초 통계량 또한 학습 데이터와 유사하게 나타나는 것을 확인할 수 있습니다.
데이터 시각화
통계만으로는 알 수 없는 데이터의 특징들이 있기 때문에 데이터를 시각화하는 작업은 매우 중요합니다. 이전에 머신러닝 카테고리에서 예시를 들어서 설명한 적도 있었죠.
앤스컴 콰르텟 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 간단한 요약 통계로 보면 동일하지만, 시각화하면 매우 다르다. 앤스컴 콰르텟(Anscombe's quartet)는 기술통계량은 유사하지만 분포나 그래프는 매우 다른 4개의 데
ko.wikipedia.org
시각화에 사용하는 라이브러리는 seaborn 과 matplotlib 입니다. 반사율 스펙트럼의 헤더값이 0~225 로 226개이기 때문에 한 번에 확인할 수 없습니다. 따라서 4개씩 맨 처음에 0, 1, 2, 3 헤더의 반사율 스펙트럼 히스토그램 분포를 확인합니다.
import seaborn as sns
import matplotlib.pyplot as plt
hist_0 = train.iloc[:,4:5]
hist_1 = train.iloc[:,5:6]
hist_2 = train.iloc[:,6:7]
hist_3 = train.iloc[:,7:8]
# 시각화를 위한 축과 크기를 설정.
f, axes = plt.subplots(2,2, figsize=(9,9), sharex=True)
# 보기 편하게 왼쪽 및 아래쪽 축을 제거.
sns.despine(left=True)
# 각각의 분포를 4개로 나눔.
sns.distplot(hist_0, kde=True, color="r", ax=axes[0,0])
sns.distplot(hist_1, kde=True, color="g", ax=axes[0,1])
sns.distplot(hist_2, kde=True, color="b", ax=axes[1,0])
sns.distplot(hist_3, kde=True, color="y", ax=axes[1,1])
plt.show()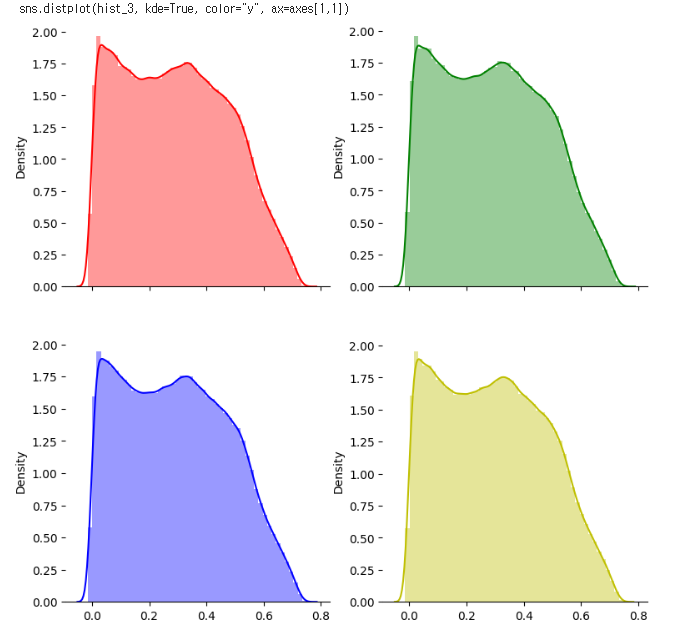
0~3 헤더 번호의 반사율 스페트럼은 비슷한 분포를 가지고 있습니다. 이 때 코드 상에서 hist_0 = train.iloc[:,4] 가 아니라 hist_0 = train.iloc[:,4:5]를 사용한 것에 대해 궁금해 찾아보았는데요, 첫 번째의 경우는 hist 가 Series 객체가 되고, 두 번째 경우는 hist 가 DataFrame 객체가 됩니다.
그래도 위처럼 단일 열에 대한 데이터를 다룰 때는 굳이 DataFrame 객체로 받아야하나? 라는 의문점이 들긴 하지만 우선은 둘이 이런 다른 점이 있구나 정도만 짚고 넘어가도록 하겠습니다.
처음 0~3 헤더의 분포가 비슷했으므로 한 번 랜덤하게 4개의 헤더를 뽑아서 분포를 확인해보도록 하겠습니다.
from random import *
# 랜덤으로 4~230 사이의 정수 4개를 뽑습니다.
random_number = randint(4,230)
print(random_number)
hist_0 = train.iloc[:,random_number:random_number+1]
random_number = randint(4,230)
print(random_number)
hist_1 = train.iloc[:,random_number:random_number+1]
random_number = randint(4,230)
print(random_number)
hist_2 = train.iloc[:,random_number:random_number+1]
random_number = randint(4,230)
print(random_number)
hist_3 = train.iloc[:,random_number:random_number+1]
f, axes = plt.subplots(2,2, figsize=(9,9), sharex=True)
sns.despine(left=True)
sns.distplot(hist_0, kde=True, color="r", ax=axes[0,0])
sns.distplot(hist_1, kde=True, color="g", ax=axes[0,1])
sns.distplot(hist_2, kde=True, color="b", ax=axes[1,0])
sns.distplot(hist_3, kde=True, color="y", ax=axes[1,1])
plt.show()
# 56
# 105
# 38
# 139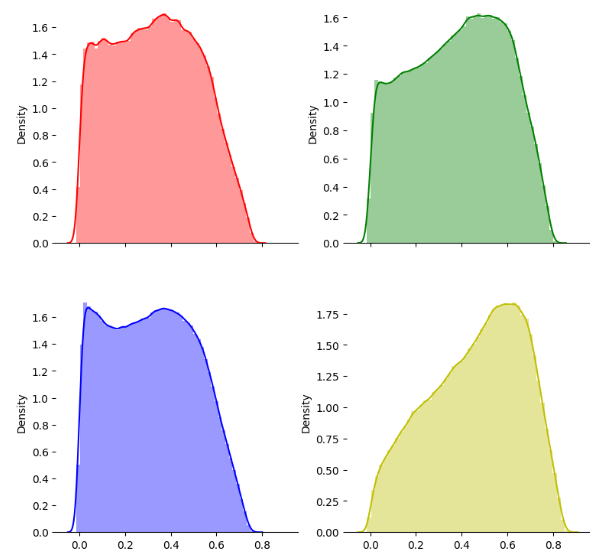
56, 105, 38, 139 번의 헤더가 선택되어서 시각화를 해보니 이전과는 다르게 여러 모양이 시각화 된 것을 확인할 수 있습니다. 반샤율 스펙트럼의 분포가 헤더별로 항상 같지는 않다는 것을 알 수 있습니다.
다음으로 학습 데이터의 박막별 두께의 분포를 시각화 하였습니다. 각 박막에 대해 어떤 두께가 가장 많은지 시각화를 통해 쉽게 알아낼 수 있습니다.
# 2x2 그리드 형태의 서브플롯 설정
fig, axes = plt.subplots(2, 2, figsize=(16, 12))
# 각각의 countplot 그리기
sns.countplot(x="layer_1", data=train, ax=axes[0, 0])
axes[0, 0].set_title("layer_1 thickness histogram")
sns.countplot(x="layer_2", data=train, ax=axes[0, 1])
axes[0, 1].set_title("layer_2 thickness histogram")
sns.countplot(x="layer_3", data=train, ax=axes[1, 0])
axes[1, 0].set_title("layer_3 thickness histogram")
sns.countplot(x="layer_4", data=train, ax=axes[1, 1])
axes[1, 1].set_title("layer_4 thickness histogram")
# 그래프 간 간격 조정
plt.tight_layout()
# 플롯 보이기
plt.show()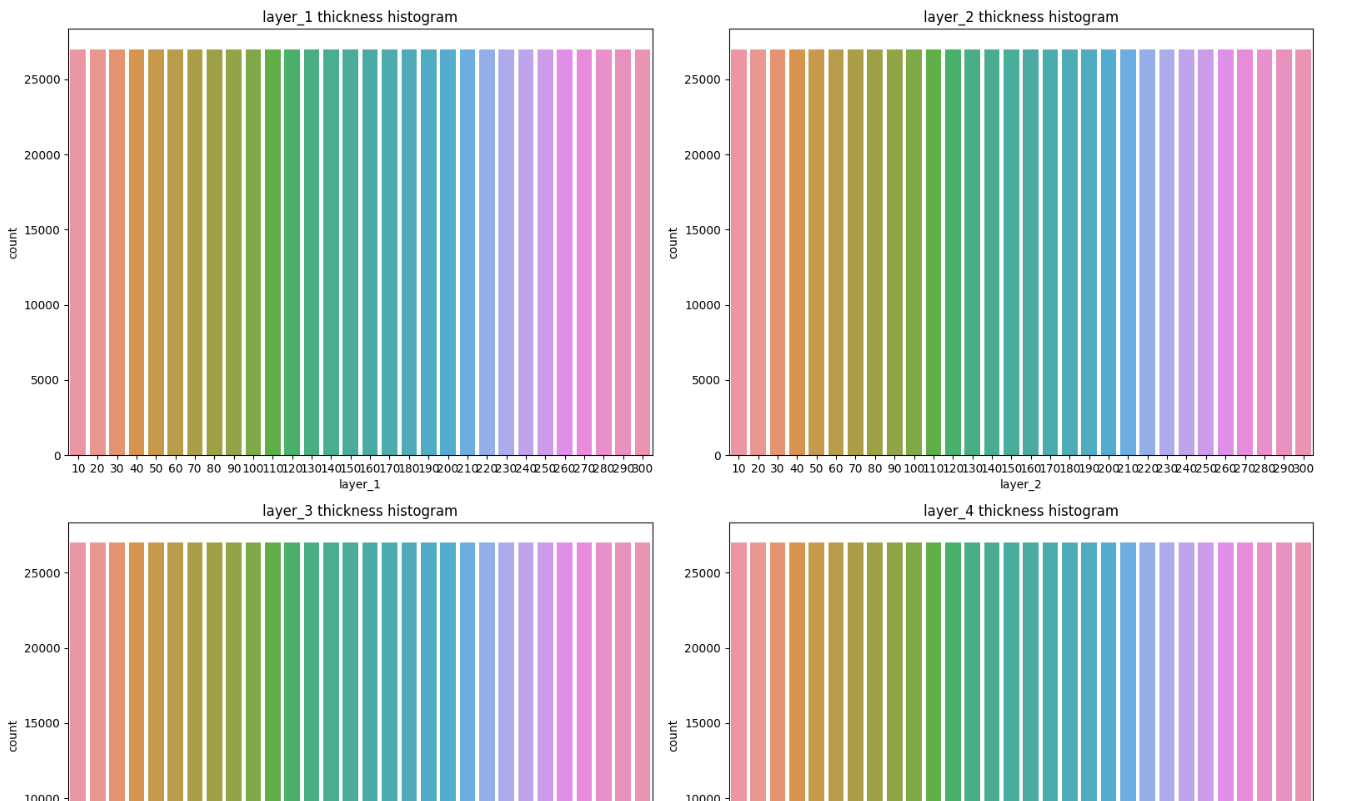
countplot()은 데이터프레임의 카테고리마다 값의 개수를 세어 출력해주는 기능을 합니다. 각 박막 번호에 대해 어떤 두께가 가장 많은지 시각화해서 보여주는 코드입니다. 하나씩 확인하려면 아래와 같은 코드를 사용해도 됩니다.
fig, ax = plt.subplots(figsize=(16,6))
sns.countplot(x="layer_1", data=train)
plt.title("layer_1 thickness histogram")
plt.show()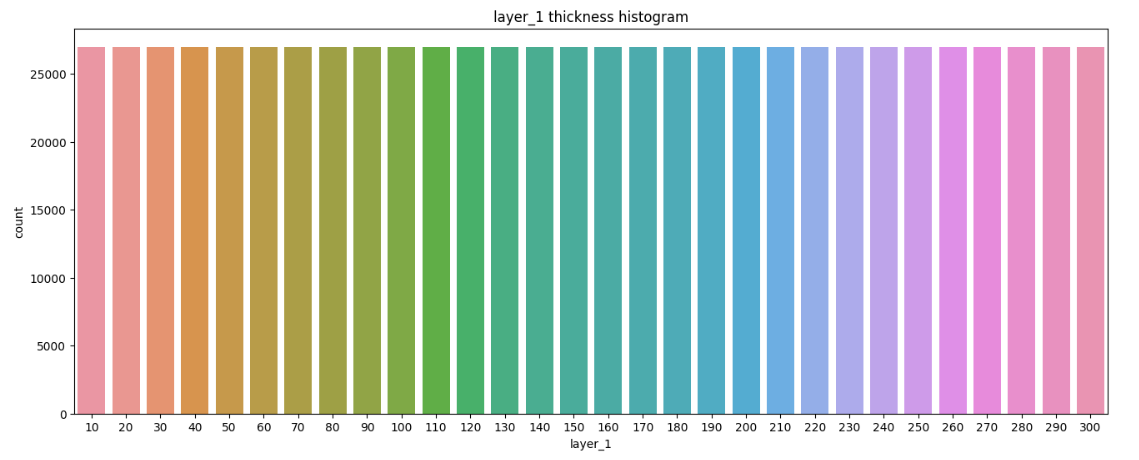
countplot()의 색상은 단순히 막대를 구분하기 위한 것으로 높이로 해석해야하는 함수입니다. 가로축에는 박막의 두께, 세로 축에는 그 두께 값이 몇 번이나 나타났는지를 표시합니다. 지금 데이터를 확인해보면 모든 히스토그램 막대의 높이가 같습니다. 이 말은 곧 모든 두께에 대해 동일한 개수의 데이터를 제공해줬다는 사실입니다. 실제 현업에서는 절대 이런 데이터가 존재하지 않겠지만 이 데이터들은 이미 전문가들에 의해 전처리가 끝난 데이터라는 사실이죠. 4개 층에 대해서도 데이터 개수가 동일하고 굉장히 균일하고 잘 처리된 데이터라는 것을 알 수 있습니다.
이미 잘 정제되어 있는 데이터가 있다면 해야할 작업은 226개의 헤더 중 예측해야 할 박막 두께에 영향을 많이 미치는 헤더가 무엇인지, 즉 상관관계를 알아내야 합니다. 판다스 라이브러리의 corr() 기능을 통해 모든 변수 간의 피어슨 상관관계를 데이터프레임으로 반환받을 수 있습니다.
cor = train.corr() # train 데이터 컬럼 간의 상관관계
display(cor.loc['layer_1':'layer_4','0':'225'].style.background_gradient(cmap='coolwarm').set_precision(2))
loc 을 통해 상관계수로부터 layer_1 ~ layer_4에 해당하는 행과 반사율 스펙트럼에 해당하는 '0':'255' 열만을 선택합니다. style.background_gradient() 는 판다스의 display() 출력 결과표에서 수치에 따라 서로 다른 배경색을 칠할 수 있게 해줍니다. cmap 은 컬러맵을 의미하며 coolwarm 은 파란색에서 빨간색으로 변하는 컬러맵입니다. 또한 set_precision(2)는 소수점 아래 둘째 자리까지만 값을 출력한다는 의미입니다.

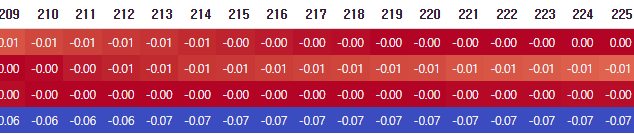
위 결과는 박막 두께와 반사율 스펙트럼 헤더들과의 피어슨 상관계수를 나타낸겁니다. 캡쳐상에서 짤렸지만 뒤쪽까지 확인해보면 225 번째 반사율 스펙트럼까지 전부 나타나있습니다.
피어슨 상관관계는 가장 많이 사용되는 상관계수의 한 종류로, -1~1 사이의 값을 가지며 피어슨 상관계수가 1일 때 양의 선형 상관관계, 0일 때 선형 상관관계 없음, -1일때 음의 선형 상관관계를 의미합니다. 즉 이를 이용해 어떤 헤더가 레이어 박막 두께에 강력한 영향을 미칠지 않을지를 알 수 있습니다.
다음으로 반사율 스펙트럼의 226개 칼럼 사이에 상관관계가 있는지를 살펴봅시다. corr()를 사용하면 데이터의 변수간 상관관계를 별도의 데이터프레임으로 제공해줍니다. 위처럼 표로만 봐서는 이를 확인하기가 어려우므로 headmap() 을 이용해 반사율 스펙트럼의 각 헤더 간의 상관 관계를 히트맵으로 출력해보도록 하겠습니다.
# 앞서 계산했던 전체 데이터의 상관관계 계수 테이블로부터 반사율 스펙트럼에 해당하는 행과 열만 선택합니다.
col_relation=cor.loc['0':'225','0':'225']
fig, ax = plt.subplots(figsize=(16,16))
sns.heatmap(col_relation, annot=False, cmap="RdBu", center=0)
plt.show()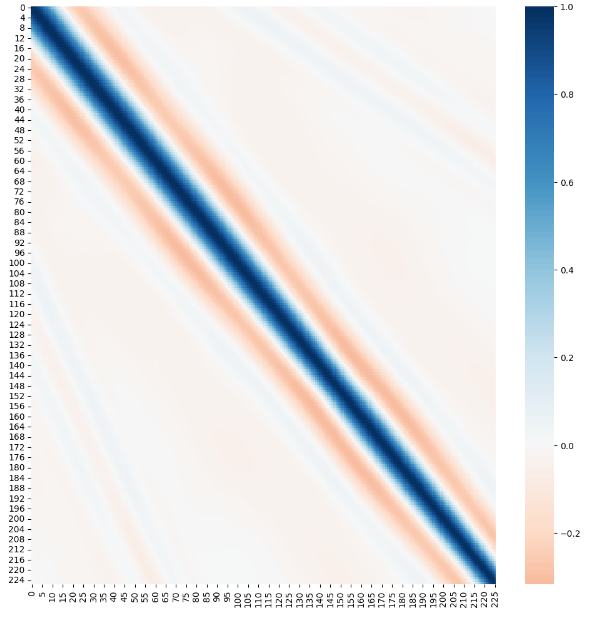
히트맵의 대각선으로 이어지는 선이 나타나는 것을 볼 수 있습니다. 한 지점을 임의로 짚어서 0번째 행과 0번째 열이 만나는 가장 왼쪽위를 확인해보면 짙은 파랑, 즉 1에 가까운 상관계수가 나타나는 것을 확인할 수 있습니다. 당연히 서로 동일한 값에 대한 상관계수는 1이 됩니다. 0번째 행을 기준으로 볼 때 행이 멀어지면 멀어질수록 점점 상관관계가 0에 가까워지다가 마침내 음수의 값을 나타냅니다. 그 뒤로 더 멀어지면 0에 가까운 상관관계를 나타내는 것을 확인할 수 있고 이 특징이 전체적인 데이터에 대해 고르게 분포되어 있습니다.
즉 변수간 번호가 가까운 칼럼 간의 상관관계는 강하게 나타나는 반면, 번호가 멀어지면 상관관계가 거의 없음을 알 수 있습니다. 전반적으로 스펙트럼도 0과 1 사이로 분포가 잘되어 있고 예측해야 하는 두께도 10 단위이며 개수까지 균일한 것으로 보아 특별한 정규화는 필요 없을 것으로 생각되고 잘 정제된 데이터세트 임을 확인할 수 있습니다.
데이터 전처리
품질이 좋지 않고 잡음이 많은 데이터로 학습을 하면 모델의 성능이 떨어질 수 있습니다. 이번 데이터는 잘 정제되어있으므로 결측치 유무만 확인하도록 하겠습니다.
null_check_train = train.isnull().sum()
null_check_test = test.isnull().sum()
print(null_check_train[null_check_train>0])
print(null_check_test[null_check_test>0])
isnull() 과 sum() 을 통해 손쉽게 NULL 값을 확인할 수 있습니다. null_check 에 대해서 train과 test 모두 빈 리스트가 출력되고 있는데 이는 곧 Null 값을 가진 결측치가 존재하지 않는다는 것을 의미합니다.
데이터 파이프라인
모델을 학습하는 단계로 이어질 수 있게 파이프라인을 구성합니다. 머신러닝에서는 모델이 설정한 하이퍼파라미터에 따라 얼마나 잘 학습했는지를 추정하고 모델 속성을 추정하기 위해 검증 데이터셋을 사용합니다.
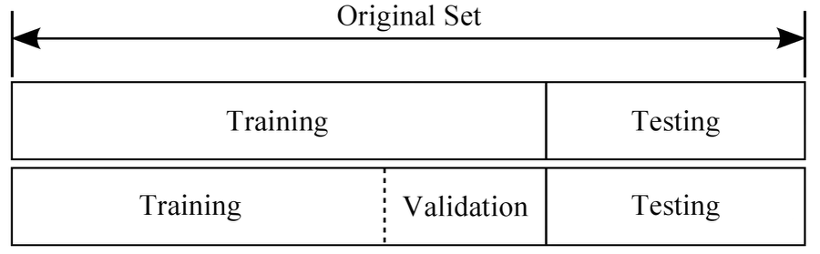
K-Fold, ShuffleSplit 등 여러 구성 방식이 있지만 이번에는 학습 데이터를 적절히 섞어 데이터의 분산이 치중되지 않게 하고 일정 범위로 나눠서 검증 데이터셋을 구성하는 간단한 방법을 사용합니다. 일반적으로 데이터를 나눌때는 8:1:1 또는 7:2:1 을 많이 사용합니다. 그런데 테스트 데이터는 이미 주어졌으므로 Train 데이터의 약 13%를 Validation dataset 으로 구성합니다.
from itertools import chain
"""
원래 제공된 학습 데이터셋에서 일정 비율을 검증 데이터셋으로 나누어 다시 저장합니다.
train.csv에 있는 데이터를 분할하여 학습 데이터는 train_splited.csv 파일에 저장하고
검증 데이터는 val.csv 파일에 저장합니다.
"""
path_train = '/content/drive/MyDrive/dacon/반도체 박막 두께 분석 경진대회_data/train.csv'
# 데이터를 섞어 다시 저장 시 인덱스 재정렬을 위한 작업을 진행합니다.
layers = [['layer_1','layer_2','layer_3','layer_4'], \
[str(i) for i in np.arange(0,226).tolist()]]
layers = list(chain(*layers))
# train의 row를 random으로 섞어줍니다.
train = pd.read_csv(path_train)
print(train.shape)
train = train.sample(frac=1)
rows, cols = train.shape
# 학습 데이터에서 일정 비율(13%)을 잘라 검증 데이터로 구성한 후 저장합니다.
train1 = train.iloc[:rows - 80000,:]
train1 = train1.values
train1 = pd.DataFrame(data=train1,columns=layers)
# 판다스 라이브러리의 to_csv() 함수를 사용해 CSV 파일로 학습 데이터를 저장합니다.
train1.to_csv('train_splited.csv', index_label='id')
print("train file saved...")
# 마찬가지로 나머지 부분은 검증 데이터를 CSV 파일로 저장합니다.
val = train.iloc[rows - 80000:,:]
val = val.values
val = pd.DataFrame(data=val,columns=layers)
val.to_csv('val.csv', index_label='id')
print("validation file saved....")
위 코드를 통해 새로 구성한 학습 데이터(train_splited.csv)와 검증(val.csv) 데이터가 생겼습니다. 앞으로 이 두 파일을 통해 모델 학습 및 검증을 진행합니다. Colab 이라면 까먹지 말고 당연히 드라이브로 옮겨서 저장을 해주셔야 합니다.
커스텀 데이터 클래스
신경망 모델에 학습시키기 적합한 형태로 데이터를 변형해주어야 합니다. 신경망의 경우 미니배치 학습을 사용하는데 이를 위해 일정량만큼의 데이터를 배치로 묶어주는 과정이 필요합니다. 이는 파이토치의 데이터로더를 사용해 이를 구현합니다.
우선 커스템 데이터 클래스를 작성합니다. 파이토치의 torch.utils.data. 에서는 Dataset 클래스를 제공합니다. Dataset 클래스 내에는 __init__(), __len__(), __getitem__() 이 포함되어 있으며 이를 상속하여 커스텀 데이터 클래스를 작성할 수 있습니다.
from torch.utils.data import Dataset
class PandasDataset(Dataset):
""" Train dataset을 가져와서 torch 모델이 학습할 수 있는 tensor 형태로 반환합니다."""
def __init__(self, path):
# 부모의 생성자를 상속
super(PandasDataset, self).__init__()
train = pd.read_csv(path).iloc[:,1:]
self.train_X, self.train_Y = train.iloc[:,4:], train.iloc[:,0:4]
self.tmp_x , self.tmp_y = self.train_X.values, self.train_Y.values
# 데이터셋 크기 리턴
def __len__(self):
return len(self.train_X)
# idx 번째의 샘플을 찾을 때 사용
def __getitem__(self, idx):
return {
'X':torch.from_numpy(self.tmp_x)[idx],
'Y':torch.from_numpy(self.tmp_y)[idx]
}위 PandasDataset 클래스의 기능은 CSV 파일을 입력받아 인덱스로 numpy로 변환된 학습 데이터를 가져오는 것입니다.
언급했듯 파이토치 프레임워크에서는 DataLoader 라는 것을 사용해 데이터셋 객체를 받아 데이터를 배치화하거나, 섞거나, 특정 가중치로 샘플링하거나 하는 기능을 할 수 있습니다. 즉 DataLoader를 사용해 불러들인 데이터를 모델의 입력으로 사용하기에 앞서 기능을 추가하고 이것 저것 설정을 할 수 있습니다. 추가적인 자세한 사항은 파이토치 공식 문서에서 확인 가능합니다.
torch.utils.data — PyTorch 2.0 documentation
torch.utils.data At the heart of PyTorch data loading utility is the torch.utils.data.DataLoader class. It represents a Python iterable over a dataset, with support for These options are configured by the constructor arguments of a DataLoader, which has si
pytorch.org
from torch.utils.data import DataLoader
from src.utils import PandasDataset
# 배치 사이즈는 하이퍼파라미터로 사용자가 직접 정의 가능.
batch_size=32
# 학습 데이터 csv와 검증 데이터 csv 경로를 지정.
train_path = '/content/drive/MyDrive/dacon/반도체 박막 두께 분석 경진대회_data/train_splited.csv'
val_path = '/content/drive/MyDrive/dacon/반도체 박막 두께 분석 경진대회_data/train_splited.csv'
# Loader를 통해 Batch 크기로 데이터를 반환합니다.
train_dataset = PandasDataset(train_path)
train_loader = DataLoader(train_dataset, batch_size=batch_size, num_workers=0)
val_dataset = PandasDataset(val_path)
val_loader = DataLoader(val_dataset, batch_size=batch_size, num_workers=0)ModuleNotFoundError: No module named 'src'
혹시 위처럼 에러가 발생한다면 필요한 폴더 및 데이터가 존재하지 않는다는 뜻입니다. 깃허브 링크로 가서 src 폴더 자체를 다운 받아서 드라이브나 코랩에 올리시면 실행이 되실겁니다.
DataLoader를 활용해 학습할 때마다 일정량을 가져올 수 있게 하는 코드입니다. num_workers 는 몇 개의 서브 프로세스를 사용해 데이터를 불러올 것인지를 나타냅니다.
모델 구축과 검증
회귀 분석에 사용할 수 있는 대표적인 신경망 모델은 MLP입니다. 베이스라인은 MLP의 기본 형태로 구성됩니다.
import torch.nn as nn
# torch.nn 모듈을 상속합니다.
class BaseLine(nn.Module):
def __init__(self):
# super()를 호출해야 BaseLine 클래스가 nn.Module의 속성을 가지고 초기화되므로
# 반드시 필요합니다.
super(BaseLine, self).__init__()
# 각 nn.Sequential()은 Dense 층, 활성 함수, 배치 정규화를 포함하고 있습니다.
self.block1 = nn.Sequential(nn.Linear(226,10000),nn.ReLU(), nn.BatchNorm1d(10000))
self.block2 = nn.Sequential(nn.Linear(10000,7000),nn.ReLU(), nn.BatchNorm1d(7000))
self.block3 = nn.Sequential(nn.Linear(7000,3000), nn.ReLU(), nn.BatchNorm1d(3000))
self.block4 = nn.Sequential(nn.Linear(3000,1000),nn.ReLU(), nn.BatchNorm1d(1000))
self.block5 = nn.Sequential(nn.Linear(1000, 300),nn.ReLU(), nn.BatchNorm1d(300))
# 마지막 출력층은 활성 함수 및 배치 정규화를 사용하지 않습니다.
self.fclayer = nn.Sequential(nn.Linear(300,4))
# forward를 정의해 위에서 정의한 노드에 입력된 x가 실제로 계산되게 정의해줍니다.
def forward(self, x):
block1_out = self.block1(x)
block2_out = self.block2(block1_out)
block3_out = self.block3(block2_out)
block4_out = self.block4(block3_out)
block5_out = self.block5(block4_out)
output = self.fclayer(block5_out)
return output
기본이 되는 MLP 모델을 클래스 형태로 재구성한 것이며 5개의 블럭으로 구성됩니다. nn.Sequential() 안쪽에 nn.Linear(), nn.ReLU(), nn.BatchNorm1d() 가 순서대로 들어있는데 이는 각각의 블록에 입력된 값이 Dense층, ReLU, 배치 정규화를 차례로 지나는 것을 의미합니다. 마지막 fclayer는 Dense층만을 이용해 총 1~4의 4개의 박막 두께를 예측해야 하므로 출력값의 개수는 4입니다. 또한 Dense층의 노드 크기는 [226, 10000, 7000, 3000, 1000, 300, 4] 순서로 변하게 됩니다.
또한 우승자 분들이 여기서 skip connection을 추가하여 학습합니다. ResNet 리뷰를 최근에 올렸었는데 그 때 올린 아이디어와 동일합니다.
Deep Residual Learning for Image Recognition (CVPR 2016)
Resnet 이란 이름으로도 유명한 이미지 분류 분야의 논문입니다. 깊이가 깊어질 수록 학습 성능이 저하되는 문제를 잔여 학습(Residual training) 이란 기법을 사용해 층이 깊어질 때 발생하는 degradation
songsite123.tistory.com
class SkipConnectionModel(nn.Module):
def __init__(self):
super(SkipConnectionModel, self).__init__()
self.upblock1 = nn.Sequential(nn.Linear(226,2000),GELU(),nn.BatchNorm1d(2000))
self.upblock2 = nn.Sequential(nn.Linear(2000,4000),GELU(),nn.BatchNorm1d(4000))
self.upblock3 = nn.Sequential(nn.Linear(4000,7000), GELU(),nn.BatchNorm1d(7000))
self.upblock4 = nn.Sequential(nn.Linear(7000,10000),GELU(),nn.BatchNorm1d(10000))
self.downblock1 = nn.Sequential(nn.Linear(10000,7000),GELU(),nn.BatchNorm1d(7000))
self.downblock2 = nn.Sequential(nn.Linear(7000, 4000),GELU(),nn.BatchNorm1d(4000))
self.downblock3 = nn.Sequential(nn.Linear(4000, 2000),GELU(),nn.BatchNorm1d(2000))
self.downblock4 = nn.Sequential(nn.Linear(2000, 300),GELU(),nn.BatchNorm1d(300))
self.dropout = nn.Dropout(0.1)
self.fclayer = nn.Sequential(nn.Linear(300,4))
def forward(self, x):
upblock1_out = self.upblock1(x)
upblock2_out = self.upblock2(upblock1_out)
upblock3_out = self.upblock3(upblock2_out)
upblock4_out = self.upblock4(upblock3_out)
# 각 층의 출력과 잔차를 더합니다.
downblock1_out = self.downblock1(upblock4_out)
skipblock1 = downblock1_out + upblock3_out # 7000
downblock2_out = self.downblock2(skipblock1)
skipblock2 = downblock2_out + upblock2_out # 4000
downblock3_out = self.downblock3(skipblock2)
skipblock3 = downblock3_out + upblock1_out # 2000
downblock4_out = self.downblock4(skipblock3)
output = self.fclayer(downblock4_out)
return output베이스라인 모델에 잔차 연결, skip connection을 추가한 모델입니다. 네트워크의 입력과 출력이 더해진 것이 다음 층의 입력으로 사용되는 구조입니다. upblock과 downblock을 정의하여 사용하는데 upblock은 정보를 증가시키는 방향으로 층을 구성하고, downblock은 upblock의 출력과 동일한 크기의 정보를 다음 층으로 넘기기 전에 합치는 역할을 합니다.
forward의 upblock 1~4는 기존 MLP와 같이 층을 통과하고 마지막 upbolck을 통과한 값이 downblock의 첫번째와 연결됩니다. 그 다음 skip block을 두어 upblock 층을 통과한 값을 downblock 층을 통과한 값에 추가로 더하는 요소별 연산을 합니다. 위 같은 과정을 순서대로 반복후 마지막 downblock4_out의 출력값이 fclayer 층을 통과해 최종 결과를 얻습니다. 또한 활성함수도 새로 정의한 GELU()를 사용하는데 이는 Gaussion Error Linear Unit 의 약자로 실험적으로 이를 사용했을 때 결과가 가장 성능이 좋아 이를 채택했다고 합니다.
class GELU(nn.Module):
def forward(self, x):
return 0.5 * x * (1 + torch.tanh(math.sqrt(2 / math.pi) * (x + 0.044715 * torch.pow(x, 3))))
그리고 일반적으로 MLP에는 드롭아웃 층을 추가하는 경우가 많은데 드롭아웃이란 설정한 확률 값에 따라 무작위로 노드를 0으로 설정하는 정규화 기법입니다. 원래 오버피팅을 방지하는 데 도움을 준다고 알려져 있어 일반적으로 사용하나 드롭 아웃층과 배치 정규화 층은 모두 정규화 기능을 포함하므로 둘 다 사용하면 오히려 학습이 떨어질 수도 있습니다. 실제로 결과를 비교하였을 때 드롭 아웃층을 안 쓴 경우가 더 좋은 성능을 나타냈다고 합니다.
성능 향상을 위한 방법
MLP를 사용할 때 배치 정규화를 사용하면 학습 속도 개선과, 가중치 초기값의 의존도 감소, 과적합 방지, 기울기 손실 문제 해결 의 이점을 볼 수 있습니다. 주로 RNN에서 배치 정규화와 비슷한 효과가 있으며 빠르게 수렴하도록 도와준다는 계층 정규화(Layer normalization)을 MLP에 적용합니다. 계층 정규화는 네트워크 각 층의 출력 분포를 정규화한다는 것을 의미합니다. 계층 정규화는 Pytorch 공식 문서에도 구현되어 있습니다.
LayerNorm — PyTorch 2.0 documentation
Shortcuts
pytorch.org
class LayerNorm(nn.Module):
def __init__(self, hidden_size, eps=1e-5):
# hidden_size 크기의 Variable을 만들어놓음
# nn.Parameter 를 사용해 autograd가 가능한 Variable 구성
super(LayerNorm, self).__init__()
self.weight = nn.Parameter(torch.ones(hidden_size))
self.bias = nn.Parameter(torch.zeros(hidden_size))
self.variance_epsilon = eps
self.init_weights()
def init_weights(self):
# x와 weight 를 곱했을 때 다시 원래의 값을 가지도록 1.0을 채움
self.weight.data.fill_(1.0)
# bias를 더했을 때 다시 원래의 값을 가질 수 있게 0을 채움
self.bias.data.zero_()
def forward(self, x):
# 마지막 차원을 기준으로 평균, 표준편차를 구함
u = x.mean(-1, keepdim=True)
s = (x - u).pow(2).mean(-1, keepdim=True)
x = (x - u) / torch.sqrt(s + self.variance_epsilon)
return self.weight * x + self.biasLayerNorm 클래스는 hidden_size를 인자로 받습니다. 층을 통과한 값들은 층의 출력 크기만큼의 크기를 갖게 되는데 hidden_size는 그 층에서 나온 크기를 의미합니다. 계층 정규화는 각 계층에서 나온 결과들을 받아 정규화합니다. 이를 사용해 위에서 보았던 SkipConnectionModel 클래스에 계층 정규화를 추가하는데, LayerNorm 클래스를 정의한 후 계층 정규화를 upblock4의 출력부터 skipblock의 결과에 적용합니다.
class SkipConnectionModel(nn.Module):
"""
>> model = Model(f_in, f_out, 300, 2000, 4000, 7000, 10000)
300, 2000, 4000, 7000, 10000 : channels
"""
def __init__(self, fn_in=226, fn_out=4, *args):
super(SkipConnectionModel, self).__init__()
self.ln = LayerNorm(10000) #10000
self.ln1 = LayerNorm(7000) # 7000
self.ln2 = LayerNorm(4000) # 4000
self.ln3 = LayerNorm(2000) # 2000
self.upblock1 = nn.Sequential(nn.Linear(fn_in, 2000),GELU(),nn.BatchNorm1d(2000))
self.upblock2 = nn.Sequential(nn.Linear(2000,4000),GELU(),nn.BatchNorm1d(4000))
self.upblock3 = nn.Sequential(nn.Linear(4000,7000), GELU(),nn.BatchNorm1d(7000))
self.upblock4 = nn.Sequential(nn.Linear(7000,10000),GELU(),nn.BatchNorm1d(10000))
self.downblock1 = nn.Sequential(nn.Linear(10000, 7000),GELU(),nn.BatchNorm1d(7000))
self.downblock2 = nn.Sequential(nn.Linear(7000, 4000),GELU(),nn.BatchNorm1d(4000))
self.downblock3 = nn.Sequential(nn.Linear(4000, 2000),GELU(),nn.BatchNorm1d(2000))
self.downblock4 = nn.Sequential(nn.Linear(2000, 300),GELU(),nn.BatchNorm1d(300))
self.fclayer = nn.Sequential(nn.Linear(300, fn_out))
self.dropout = nn.Dropout(0.1)
def forward(self, x):
upblock1_out = self.upblock1(x)
upblock2_out = self.upblock2(upblock1_out)
upblock3_out = self.upblock3(upblock2_out)
upblock4_out = self.upblock4(upblock3_out)
# upblock에서 나온 결괏값들의 정규화를 진행합니다.
downblock1_out = self.downblock1(self.ln(upblock4_out))
skipblock1 = downblock1_out + upblock3_out
downblock2_out = self.downblock2(self.ln1(skipblock1))
skipblock2 = downblock2_out + upblock2_out
downblock3_out = self.downblock3(self.ln2(skipblock2))
skipblock3 = downblock3_out + upblock1_out
downblock4_out = self.downblock4(self.ln3(skipblock3))
output = self.fclayer(downblock4_out)
return output실험을 통해 SkipConnectionModel 에 계층 정규화 층을 추가한 모델이 가장 좋은 성능을 보였기 때문에 최종 신경망 모델로 사용했다고 합니다.
추가적으로 최종 모델을 정하더라도 성능을 위해 다양한 실험을 해볼 수 있습니다. 활성 함수의 변경 및 노드의 수와 깊이 변경, 최적화 함수, 초기 학습률 지정, 스케줄러 등의 변경으로 구분할 수 있습니다. 마지막으로 위 같은 것들을 변경해보고 앙상블을 통해 학습한 모델들을 결합하여 좋은 성능을 나타냈다고 합니다.
옵티마이저 및 스케줄러 조정
from torch.optim.lr_scheduler import LambdaLR
"""
학습 최적화를 위해 스케줄러를 활용합니다.
Pytorch 및 transformer의 스케줄러를 참고.
https://github.com/huggingface/transformers/blob/master/src/transformers/optimization.py
"""
def get_cosine_with_hard_restarts_schedule_with_warmup(
optimizer, num_warmup_steps, num_training_steps, num_cycles=1.0, last_epoch=-1
):
""" 학습률이 웜업 기간 이후 몇 번의 하드 리스타트를 하는 코사인 함수 값에 따라 감소하는
스케줄러를 만듭니다. 웜업 기간에는 학습률이 0과 1 사이에서 선형으로 증가합니다.
"""
def lr_lambda(current_step):
if current_step < num_warmup_steps:
return float(current_step) / float(max(1, num_warmup_steps))
progress = float(current_step - num_warmup_steps) / \
float(max(1, num_training_steps - num_warmup_steps))
if progress >= 1.0:
return 0.0
return max(0.0, \
0.5 * (1.0 + math.cos(math.pi * ((float(num_cycles) * progress) % 1.0))))
return LambdaLR(optimizer, lr_lambda, last_epoch)역전파에서 손실 값을 최소로 줄여 신경망 퍼셉트론의 계수를 최적화할 때 적절한 옵티마이저를 선택하는 것도 중요합니다. SGD, Adam이 많이 사용되지만 실험을 통해 AdamW를 이용했고, AdamW는 Adam보다 일반화 성능 개선에 효과가 있다고 알려진 옵티마이저입니다. 옵티마이저의 학습률을 학습 단계별로 조절하기 위한 스케줄러를 정의해 사용하였는데 이 또한 여러 개의 스케줄러를 실험하여 가장 좋은 점수를 얻은 코사인 스케줄러를 선택했다고 합니다.
코사인 학습 스케줄러는 웜업 기간 내에서는 학습률이 선형으로 증가하고, 이 기간 이후 몇번의 hard restart를 거쳐 코사인 에 따라 학습률이 감소하는 스케줄러입니다.
import os
import time
from tqdm.auto import tqdm
from torch.optim import AdamW
# 모델을 학습시키기 위한 하이퍼 파라미터를 설정합니다.
lr = 1e-03
adam_epsilon = 1e-06
batch_size = 2048
warmup_step = 2000
epochs = 4
# 모델 학습 데이터 경로를 설정합니다.
train_path = '/content/drive/MyDrive/dacon/반도체 박막 두께 분석 경진대회_data/train_splited.csv'
val_path = '/content/drive/MyDrive/dacon/반도체 박막 두께 분석 경진대회_data/train_splited.csv'
# Loader를 통해 Batch 데이터로 반환합니다.
train_dataset = PandasDataset(train_path)
train_loader = DataLoader(train_dataset, batch_size=batch_size, num_workers=0)
val_dataset = PandasDataset(val_path)
val_loader = DataLoader(val_dataset, batch_size=batch_size, num_workers=0)
# 모델이 학습하는 전체 step을 계산합니다.
total_step = len(train_loader) * epochs
print(f"Total step is....{total_step}")
그 이후 학습을 진행하는 기본적인 코드가 나타납니다. 필요한 라이브러리들을 불러오고 하이퍼 파라미터 및 경로의 설정, 학습 전 데이터 준비까지 한 코드입니다. 앞서 정의한 커스텀 데이터 반환 클래스의 객체를 만들어주고, 이후 데이터셋 객체를 데이터 로더 객체에 넣어 정의합니다. 이 객체는 학습 데이터의 길이에 맞춰 앞서 정의한 배치 수만큼 반환합니다. 검증하기 위한 validation 데이터셋에 대해서도 동일한 과정을 반복합니다.
이처럼 모델이 불러온 데이터에 대해서 한 번 학습하는 것을 '스텝(step)' 이라 합니다. 모델은 전체 데이터에서 배치로 묶은 학습을 진행하므로 데이터 샘플 총 개수에서 배치 수만큼 나누어주면 모델이 한 번 학습하는 스텝의 수를 알 수 있습니다. 로더에서 앞선 과정이 계산돼었으므로 데이터 로더의 크기를 모델이 모든 데이터 샘플을 한 번 학습하는 스텝의 수로 볼 수 있습니다. 여기에 반복하고 싶은 만큼 곱해주면 모델이 학습하는 총 스텝수를 구할 수 있습니다. 실제 에포크가 100 정도 되었는데 저는 간단히 돌려볼 예정이라서 epoch 를 4로만 설정했습니다.
# 모델 인스턴스를 정의합니다.
model = SkipConnectionModel(fn_in=226, fn_out=4) # channel은 모델에서 수정합니다.
# GPU 및 CUDA 환경이 마련되어 있다면, 모델 학습을 위해 CUDA 환경을 직접 설정합니다.
# 그렇지 않은 경우 자동으로 CPU를 설정하게 됩니다.
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 모델을 GPU 메모리에 올립니다. gpu가 없는 환경은 자동으로 cpu가 설정됩니다.
model = model.to(device)
# 손실함수와 옵티마이저
# 신경망 모델을 최적화할 수 있게 손실함수를 정의합니다.
# MAE를 사용합니다.
loss_fn = nn.L1Loss()
# 옵티마이저와 스케줄러의 파라미터를 정의합니다.
no_decay = ["bias", "LayerNorm.weight"] # decay하지 않을 영역 지정
optimizer_grouped_parameters = [
{
"params": [p for n, p in model.named_parameters() \
if not any(nd in n for nd in no_decay)],
"weight_decay": 0.0,
},
{"params": [p for n, p in model.named_parameters() \
if any(nd in n for nd in no_decay)], "weight_decay": 0.0},
]
# 옵티마이저와 스케줄러 객체를 정의합니다.
optimizer = AdamW(optimizer_grouped_parameters, lr=lr, eps=adam_epsilon)
scheduler = get_cosine_with_hard_restarts_schedule_with_warmup(
optimizer, num_warmup_steps=warmup_step, num_training_steps=total_step
)그 다음으로 학습에 필요한 모델과 최적화 함수를 준비합니다. 앞서 정의했던 SkipConnectionModel 클래스를 호출하고, torch에서 L1 Loss 객체를 정의합니다. 모델의 파라미터 최적화를 위한 옵티마이저 AdanW 객체를 정의하고 일반화 성능을 높이기 위해 weight_decay를 지정합니다. 일단 0.0으로 지정하여 weight decay를 진행하지 않았고, 이에 대한 세부내용은 추후 포스팅을 하게 되면 링크를 걸도록 하겠습니다.
이제 학습을 하면 됩니다.
# 모델 이름을 위해서 변수를 만듭니다.
version = time.localtime()[3:5]
curr_lr = lr
# train loss와 val loss를 지정합니다.
total_loss = 0.0
total_val_loss = 0.0
n_val_loss = 10000000. # best validation loss를 저장하기 위해서 변수 설정합니다.
if not os.path.exists('bin'):
os.mkdir('bin')
for epoch in range(epochs):
total_loss = 0
total_val_loss = 0
for i, data in enumerate(tqdm(train_loader, desc='*********Train mode*******')): # train 데이터를 부르고 학습합니다.
# 학습 데이터를 부르고 학습합니다.
# 순방향 정의
pred = model(data['X'].float().to(device))
loss = loss_fn(pred, data['Y'].float().to(device))
# 역방향 정의
# optimizer 객체를 사용해서 학습 가능한 가중치 변수에 대한 모든 변화도를
# 0으로 만듭니다.
optimizer.zero_grad()
# loss에 따른 오차 역전파를 구합니다.
loss.backward()
# optimizer 객체의 파라미터들을 업데이트합니다.
optimizer.step()
# scheduler 객체의 파라미터들을 업데이트합니다.
scheduler.step()
total_loss += loss.item()
train_loss = total_loss / len(train_loader)
print ("Epoch [{}/{}], Train Loss: {:.4f}".format(epoch+1, epochs, train_loss))
# 평가
# 검증 데이터를 부르고 에포크마다 학습된 모델을 부르고 평가합니다.
model.eval()
with torch.no_grad():
for i, data in enumerate(tqdm(val_loader, \
desc='*********Evaluation mode*******')):
pred = model(data['X'].float().to(device))
loss_val = loss_fn(pred, data['Y'].float().to(device))
total_val_loss += loss_val.item()
val_loss = total_val_loss / len(val_loader)
print ("Epoch [{}/{}], Eval Loss: {:.4f}".format(epoch+1, epochs, val_loss))
# 검증 데이터에서 가장 낮은 평균 절대 오차를 보인 에포크의 모델을 저장합니다.
if val_loss < n_val_loss:
n_val_loss = val_loss
#torch.save(model.state_dict(), f'bin/test_{version}.pth')
torch.save(model.state_dict(), f'bin/test.pth')
print("Best Model saved......")
핵심은 두 번째 for문으로 학습 데이터를 불러와 model의 출력값인 pred를 실제 정답인 data['Y']와 정의해놓은 손실 함수에서 발생한 차이를 통해 손실을 구합니다. 이 때 손실은 단일 스칼라 값이고, 이 스칼라 값을 torch가 역전파 그래프에 전달해 역전파를 수행합니다. 이것이 loss, backward()를 통해 진행됩니다. 이 과정을 통해 각 파라미터의 local gradient가 구해지면 반대방향으로 파라미터가 업데이트되는데 이 과정을 최적화한다고 하며 optimizer.step() 으로 진행됩니다. 이렇게 구해진 loss가 잘 학습되고 있는지 확인하기 위해 학습 손실을 정의하고 배치마다 계산된 loss를 합산한뒤, 에포크마다 평균을 내어 구해줍니다.
학습이 끝나고 나면 검증 데이터셋을 통해 확인해봅니다. 이 과정은 당연히 학습이 한 번 끝났을 때 진행되는 것이며, model.eval()을 통해 모델의 파라미터를 고정하고 미리 정의했던 val 데이터셋을 이용해 동일한 과정을 반복합니다. 이 때 검증 데이터셋으로는 학습을 하지 않으므로 loss.backward()와 optimezer.step() 과정을 진행하지 않습니다. 마지막을 성능 비교하면서 학습했는데 이전 모델보다 검증 성능이 더 좋지 않다면 저장하지 않습니다.
4번 밖에 학습을 안했음에도 불구하고 처음에는 153.7864가 나오던 Loss가 4번째 학습이 끝난 이후에는 6.08정도가 나옵니다. 이 데이터 세트가 굉장히 잘 정제되어 있고 큰 데이터라서 더욱 이렇게 잘 학습되는 것으로 유추합니다.
위의 학습한 모델을 불러와서 테스트 데이터로 submission 파일을 만들어 봅시다.
# 모델 평가 시 GPU를 사용하기 위해서 설정.
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 테스트 데이터 위치
path_test = '/content/drive/MyDrive/dacon/반도체 박막 두께 분석 경진대회_data/test.csv'
# pth 파일(모델 한 개 예시)
# 학습을 통해 저장된 pth 파일을 가져옵니다.
pth_bin = 'bin/test.pth'
# Test Model
# 모델을 테스트하기 위해서 모델을 다시 정의합니다.
test_model = SkipConnectionModel(fn_in=226, fn_out=4)
test_model = test_model.to(device)주석 그대로 학습되었던 모델에 이제 테스트 데이터를 입력으로 넣을 것이기 때문에 모델을 재정의 해줍니다.
# Test dataset을 불러옵니다.
test_data = TestDataset(path_test)
test_loader = DataLoader(test_data, batch_size=10000, num_workers=0)
# 테스트 데이터를 불러와서 모델로 결과를 예측하고 그 결과를 파일로 씁니다.
with torch.no_grad():
for data in test_loader:
data = data.to(device)
outputs = test_model(data.float())
pred_test = outputs또한 테스트 단계에서는 이미 학습한 가중치를 업데이트하면 안되기 때문에 불러온 모델에 torch.no_grad 를 적용해서 역전파가 안되게 해야합니다. test_loader 에서 테스트 데이터를 불러와 테스트 데이터가 모델에 통과되었을 때의 최종 결과를 outputs로 반환받습니다.
sample_sub = pd.read_csv('/content/drive/MyDrive/dacon/반도체 박막 두께 분석 경진대회_data/sample_submission.csv', index_col=0)
layers = ['layer_1','layer_2','layer_3','layer_4'] # 데이터의 컬럼명을 정의해줍니다.
submission = sample_sub.values + pred_test.cpu().numpy() # 파일을 쓸 때 CPU에서 진행합니다.
submission = pd.DataFrame(data=submission,columns=layers)
submission.to_csv('.submission.csv', index_label='id')마지막으로 반환받은 outputs를 CSV 파일 형식으로 써서 저장합니다. 그리고 이 파일을 제출하면 끝입니다!
앙상블
앙상블이란 다양한 종류의 모델을 결합해 개별 모델의 결과보다 더 우수한 성능을 얻는 것입니다. 앙상블의 여러 기법 중 보팅(voting) 기법을 사용하였고, 보팅 기법 또한 두 가지로 구분됩니다. 여러 모델에서 예측한 값 중 다수의 모델에서 예측한 결과값을 최종적으로 선택하는 하드 보팅(hard voting) 과 여러 모델의 예측 확률값을 모두 더한 후 평균값을 통해 최종적으로 선택하는 소프트 보팅(soft voting) 이 있습니다.
이 대회 우승자의 경우 회귀 문제이기 때문에 소프트 보팅을 이용해 앙상블을 사용했다고 소개했습니다. 하드 보팅은 클래스 분류 문제 같은 경우 유용하게 사용됩니다. 그래서 간단한 하드 보팅과 소프트 보팅의 예제 코드를 보고 마무리하도록 하겠습니다.
output_1 = [0.7, 0.1, 0.2]
output_2 = [0.5, 0.2, 0.3]
output_3 = [0.3, 0.4, 0.3]
def hard_voting(output_1, output2, output_3):
result = [0,0,0]
# 각 output에서 가장 큰 수의 인덱스를 찾습니다.
output_1_max_value = max(output_1)
output_1_max_index = output_1.index(output_1_max_value)
result[output_1_max_index] += 1
output_2_max_value = max(output_2)
output_2_max_index = output_2.index(output_2_max_value)
result[output_2_max_index] += 1
output_3_max_value = max(output_3)
output_3_max_index = output_3.index(output_3_max_value)
result[output_3_max_index] += 1
return result
result = hard_voting(output_1, output_2, output_3)
print(result)
# 출력 : [2, 1, 0]하드 보팅의 경우 각 신경망의 출력 확률값 중 가장 높은 클래스를 선택한 후 투표합니다. output이 3개 있을 때 순서대로 A,B,C 라고 하면 최종적으로 [2, 1, 0] 으로 출력값이 나오게 되어 A를 선택하는 방식입니다.
output_1 = [0.7, 0.1, 0.2]
output_2 = [0.5, 0.2, 0.3]
output_3 = [0.3, 0.4, 0.3]
def soft_voting(output_1, output2, output_3):
result = [0,0,0]
# 각 output의 소프트 맥스 확률을 더합니다.
result = [(x+y+z)/3 for x,y,z in zip(output_1, output_2, output_3)]
return result
result = soft_voting(output_1, output_2, output_3)
print(result)
# 출력 : [0.5, 0.233, 0.266]소프트 보팅은 각 신경망의 출력 확률값을 클래스 별로 더한 후 평균 내어 가장 높은 값을 선택하는 방식입니다.
여기까지 반도체 박막 두께 분석 경진대회 우승 코드 리뷰를 해보면서 Colab으로 돌려보기 까지 해봤습니다. 처음으로 데이콘 코드를 분석한 소감은... 앞으로 배워야 할 내용이 정말 많다라는 생각이 드네요. 그래도 어떤 구조로 진행되는지 전체적인 내용을 다룰 수 있고, 또 최근 공부한 내용들이 적용이 되는 것을 보니 흥미롭기도 한 리뷰였습니다. 이번 데이콘의 경우는 데이터가 너무 잘 정제되어 있어 전처리 같은 부분이 거의 없었는데, 다음 데이콘 리뷰는 조금 더 러프한 데이터세트를 주고 전처리에 힘을 쏟은 우승 코드를 찾아서 리뷰하도록 하겠습니다. 감사합니다.

Reference :
https://pytorch.org/docs/stable/generated/torch.nn.LayerNorm.html
https://arxiv.org/pdf/1607.06450.pdf
https://dacon.io/codeshare/651
https://pytorch.org/docs/stable/data.html
https://dacon.io/competitions/official/235554/data/
https://github.com/wikibook/dacon/tree/master/