이진 탐색 트리(Binary Search Tree)
[C 자료구조] 트리(Tree) 의 종류
트리(Tree) 란? 수학, 그래프 이론에서는 회로가 없는 무방향의 그래프를 트리라고 정의합니다. 이는 자료구조에서 쓰이는 트리와 기본적으로 같지만 차이가 좀 있습니다. 무슨 말인지 쉽게 알아
songsite123.tistory.com
트리와 이진트리의 개념은 위 포스팅에서 확인하시면 되겠습니다. 이진탐색트리는 빠른 탐색 및 정렬을 위해 고안된 형태의 자료구조로 어떠한 특징을 가지는 이진트리를 말합니다.
- 각 노드에 중복되지 않는 키(key)가 있다.
- 루트 노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 값을 가지고 있다.
- 루트 노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 값을 가지고 있다.
- 좌우 서브 트리도 모두 이진 탐색 트리이다.
이 조건들을 한 줄로 정리하면 key(왼쪽서브트리) ≤ key(루트노드) ≤ key(오른쪽서브트리) 가 전체 트리에 걸쳐 적용되는 트리를 말합니다.
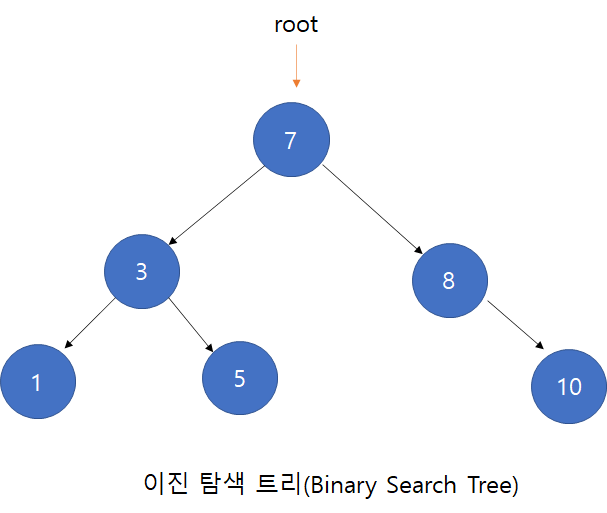
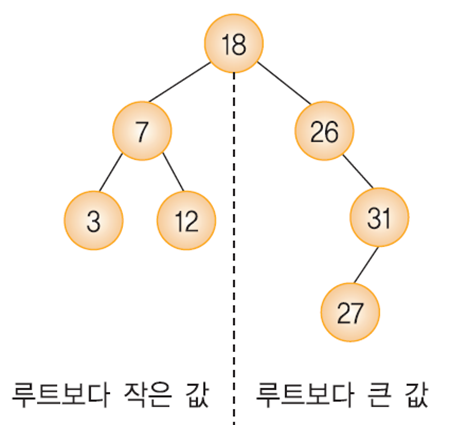
위 같은 트리를 이진 탐색 트리라고 합니다.
이진 탐색 트리는 기존 이진트리보다 탐색이 빠릅니다. 또한 이진 탐색 트리를 중위순회하게 되면 오름차순으로 정렬된 값을 얻을 수 있기 때문에 정렬에도 유리합니다. 이진 탐색 트리의 탐색 연산은 트리의 높이가 h 라면 O(h)의 시간 복잡도를 가지게 됩니다. 이런 효율적인 탐색이 가능한 이유는 아래에서 탐색 과정을 보면서 이해해보도록 하겠습니다.
이진 탐색 트리 탐색 ( Search of Binary Search Tree )
이진 탐색 트리에서의 탐색은 아래의 과정을 거칩니다.
- 루트 노드의 키와 찾고자 하는 값을 비교한다. 찾고자 하는 값이라면 탐색을 종료한다.
- 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행한다.
- 찾고자 하는 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리로 탐색을 진행한다.
위 과정을 찾고자 하는 값을 찾을 때까지 반복해서 진행합니다. 만약 값을 찾지 못하면 그대로 종료합니다.
이러한 탐색 과정을 거치면 최대 트리의 높이(h) 만큼의 탐색이 진행되게 됩니다. 그리고 이 과정은 이진 탐색 알고리즘과 굉장히 유사한 특성을 지니고 있습니다.
이진 탐색(Binary search) 알고리즘
이진 탐색은 정렬된 리스트에서 검색 범위를 줄여나가면서 검색 값을 찾는 알고리즘 입니다. 혹시 여러분 ...
blog.naver.com
이진 탐색 트리의 탐색 과정을 단계별로 알아보도록 합시다.
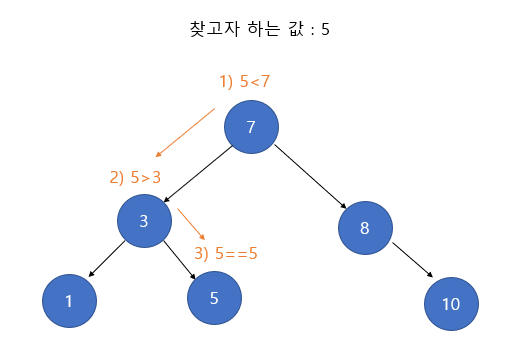

만약 왼쪽의 이진 탐색 트리에서 키가 5인 노드를 찾고 싶다면 가장 먼저 루트 노드와의 비교가 이루어집니다. 5가 7보다 작으므로 왼쪽 서브트리로 탐색이 이루어지고, 다시 5와 3을 비교하여 5가 3보다 크므로 오른쪽 서브 트리로 탐색이 이루어진다. 위 같은 경우는 5라는 값을 찾았으므로 탐색이 종료됩니다. 즉 트리의 높이인 h 만큼의 탐색이 이루어졌습니다. 만약 3이라는 값을 찾으려고 했으면 2번의 비교 연산만으로 탐색이 종료되었을 것입니다. 즉 트리 안의 값을 찾을 때는 무조건 높이(h) 이하의 탐색이 이루어지게 됩니다.
이진 탐색 트리의 탐색 구현
이진 탐색 트리의 탐색은 2가지 방법으로 구현할 수 있습니다. 바로 재귀적으로 구현하는 방법과 반복문을 사용하여 구현하는 방법입니다. 순회와 마찬가지로 재귀적으로 구현하는 방법은 코드가 직관적이고 간편해 빠르고 쉽게 짤 수 있다는 장점이 있고, 반복문을 통해 짜는 방법은 일반적으로 조금 더 복잡하고 덜 직관적이지만 더 빠르고 메모리 용량도 덜 쓰는 성능적인 장점을 가지고 있습니다. 그러나 탐색의 경우 재귀적 구현이나 반복문 구현이나 복잡도가 거의 비슷하기 때문에 가능하면 반복문을 통해 구현하여 사용하는 것이 좋습니다.
순환적 방법 ( 재귀적 구현 )
TreeNode* search(TreeNode* node, int key)
{
if (node == NULL) return NULL;
if (key == node->key)
return node;
else if (key < node->key)
return search(node->left, key);
else
return search(node->right, key);
}재귀적으로 구현하면 매우 직관적입니다. key 가 찾는 값이라면 그대로 반환, 키가 더 작다면 왼쪽 노드로 다시 탐색 진행, 키가 더 크다면 오른쪽으로 다시 탐색을 진행하면 끝입니다.
반복적 방법 ( 반복문 구현 )
TreeNode* search(TreeNode* node, int key)
{
while (node != NULL) {
if (key == node->key) return node;
else if (key < node->key)
node = node->left;
else
node = node->right;
}
return NULL; // 탐색 실패인 경우 NULL 반환
}재귀적 구현과 거의 동일하나 NULL 포인터를 만날 때까지 반복하는 while 문이 있다는 점만 다릅니다. 내부의 내용은 위와 동일하고, 함수를 호출하는 것이 아닌 node 의 이동만 진행합니다. 함수를 단계별로 분석해보면 먼저 매개변수 node가 NULL이 아니면 계속 반복을 합니다. 그 다음은 key 값 비교를 통해 node 가 변경되고 node 가 결국 단말노드까지 내려가서 NULL 값이 될때까지 반복됩니다. 여기서 함수의 매개변수 node 를 직접 사용하였는데, 매개변수는 원본 변수의 복사본이므로 원본 변수에는 영향을 주지 않습니다.
이진 탐색 트리 삽입 연산
이진 탐색 트리에서의 삽입 연산은 탐색과 비슷한 과정을 거칩니다. 단계별로 이를 나타내면
- 삽입할 값을 루트 노드와 비교해 같다면 오류를 발생한다. (이진 탐색 트리는 중복된 키값 허용 X)
- 삽입할 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.
- 삽입할 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.
아래의 트리에 6을 키로 가진 노드를 추가하는 과정을 살펴봅시다.

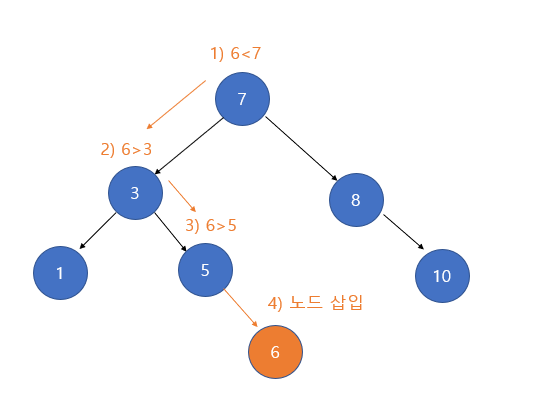
탐색과 비슷하게 삽입할 위치를 계속 비교해서 찾습니다. 삽입할 위치가 5의 오른쪽 서브트리 인 것을 찾았으므로 5의 오른쪽 자식으로 6을 추가하면 됩니다.
TreeNode* new_node(int item)
{
TreeNode* ptr = (TreeNode*)malloc(sizeof(TreeNode));
ptr->key = item;
ptr->left = ptr->right = NULL;
return ptr;
}
TreeNode* insert_node(TreeNode* node, int key)
{
// 트리가 공백이면 새로운 노드 반환
if (node == NULL) return new_node(key);
// 그렇지 않다면 순환적으로 트리를 내려간다.
if (key == node->key) fprintf(stderr, "중복 key 값 오류\n");
else if (key > node->key)
node->left = insert_node(node->left, key);
else
node->right = insert_node(node->right, key);
// 변경된 루트 포인터를 반환
return node;
}
이진 탐색 트리 삭제 연산
노드를 삭제하는 것이 이진 탐색 트리에서 가장 복잡한 연산입니다. 먼저 노드를 삭제하기 위해 노드를 탐색하는 것은 삽입과 동일합니다. 우리가 삭제하려는 값이 트리에서 어느 위치에 있는지를 알아야 지울 수 있죠. 노드를 탐색했다면 3가지 경우에 대해 고려해야 합니다.
- 삭제하려는 노드가 단말 노드인 경우
- 삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리를 가지고 있는 경우
- 삭제하려는 노드가 두 개의 서브트리 모두를 가지고 있는 경우
첫 번째와 두 번째는 간단한데, 세 번째 경우가 조금 복잡합니다. 단계별로 알아보도록 하겠습니다.
삭제하려는 노드가 단말 노드인 경우
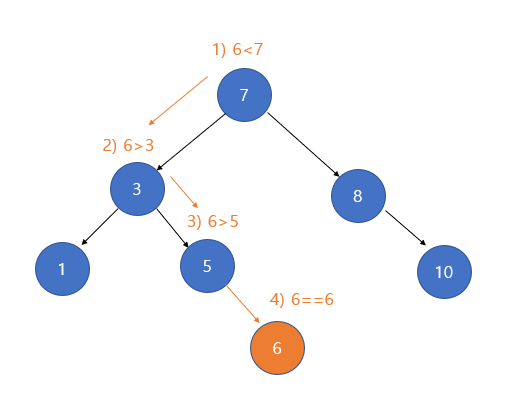
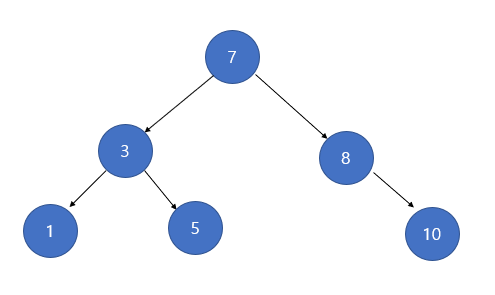
자식이 없는 단말 노드의 경우 삭제는 간단합니다. 탐색을 통해 위치를 찾았다면 단말 노드만 지우면 됩니다. 단말 노드를 지운다는 것은 단말 노드의 부모 노드를 찾아서 부모노드안의 포인터 연결을 NULL 포인터로 만들어서 연결을 끊어주면 됩니다. 그리고 동적으로 노드를 생성했다면 단말 노드를 메모리 해제 시키면 끝납니다.
삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리를 가지고 있는 경우
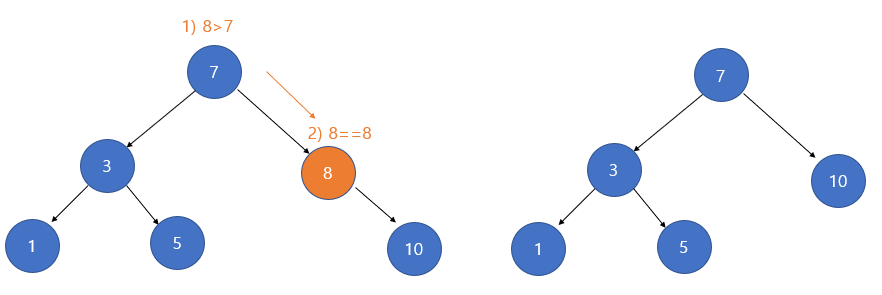
이 경우까지도 직관적으로 어렵지 않습니다. 삭제되는 노드가 왼쪽 혹은 오른쪽 서브 트리 중 하나만 가지고 있는 경우에는 자기 노드는 삭제하고 서브 트리는 자기 노드의 자기 노드의 부모 노드에 붙여주면 됩니다. 이 과정은 연결리스트에서 중간에 있는 노드의 삭제와 매우 유사합니다.
삭제하려는 노드가 두 개의 서브트리 모두를 가지고 있는 경우
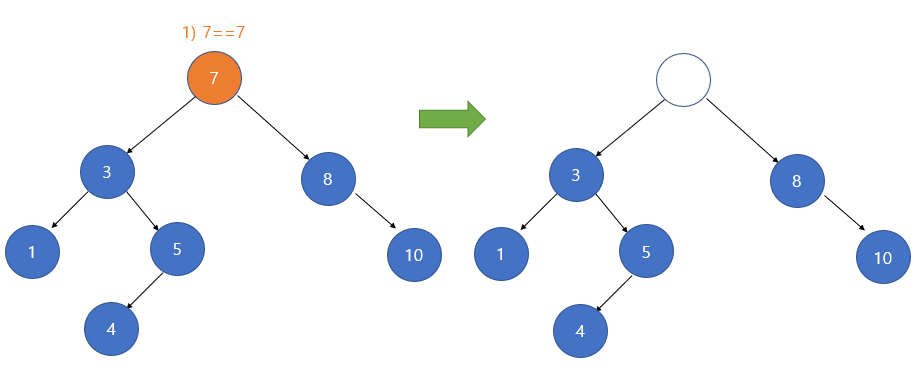
이 경우가 복잡합니다. 만약 노드를 삭제 시키고 난 이후 그 자리에는 어떤 노드가 들어가야 할까요? 비슷한 노드를 그 자리로 이동시켜야만 이진 탐색 트리가 그대로 유지됩니다. 가장 값이 가까운 노드는 왼쪽 서브 트리에서 가장 큰 값이나 오른쪽 서브 트리에서 가장 작은 값이 됩니다. 이 값들은 이진 탐색 트리를 중위 순회(LVR) 할 경우 선행 노드와 후속 노드에 해당합니다. 이 둘 중에서는 어떤 값을 선택해도 무방합니다.
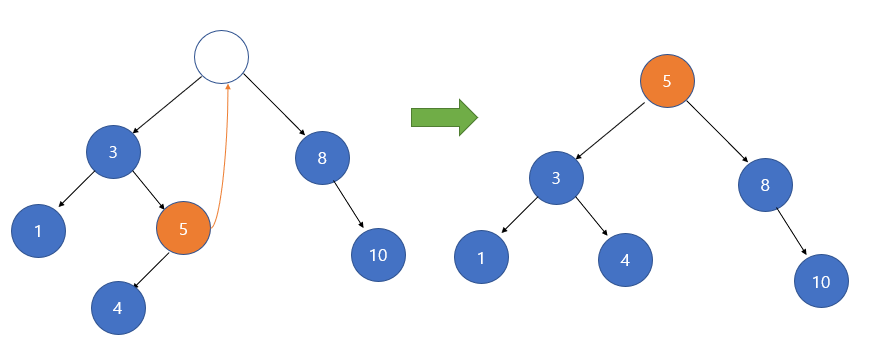
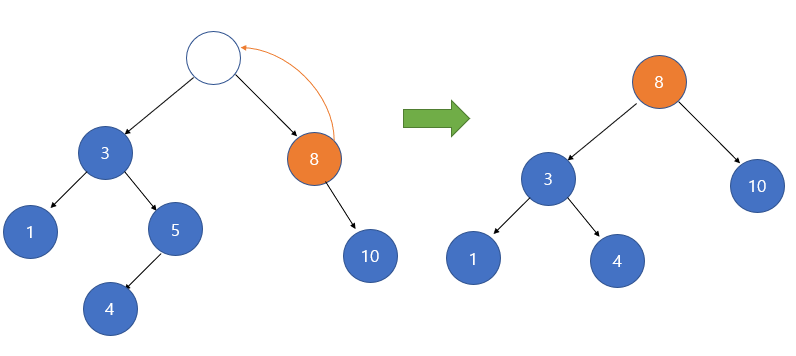
아래의 소스 코드는 오른쪽 서브 트리에서 제일 작은 값을 올리는 코드입니다. 이 때 올리는 노드를 후계자 노드(successor node) 라고도 부릅니다.
TreeNode* min_value_node(TreeNode* node)
{
TreeNode* current = node;
// 맨 왼쪽 단말 노드 탐색
while (current->left != NULL)
current = current->left;
return current;
}
TreeNode* delete_node(TreeNode* root, int key)
{
if (root == NULL) return root;
if (key < root->key)
root->left = delete_node(root->left, key);
else if (key > root->key)
root->right = delete_node(root->right, key);
else { // 키가 루트와 같다면 이 노드를 삭제
// 자식 노드가 0개 혹은 1개인 경우
if (root->left == NULL) {
TreeNode* temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL) {
TreeNode* temp = root->left;
free(root);
return temp;
}
// 자식 노드가 2개인 경우
TreeNode* temp = min_value_node(root->right); // 오른쪽 서브트리에서 가장 작은 값 탐색
// 중위 순회 시 후계 노드를 복사 (오른쪽 서브트리에서 가장 작은 값을 복사)
root->key = temp->key;
// 중위 순회 시 후계 노드를 삭제한다.
root->right = delete_node(root->right, temp->key);
}
return root;
}다 이해할만 한데 마지막에 3줄이 조금 이해하기 힘듭니다. 단계별로 마지막 3줄만 해석해보도록 하겠습니다.
먼저 min_value_node 는 그 트리에서의 최솟값을 찾는 함수입니다. 이진 탐색 트리의 경우 가장 왼쪽 데이터가 그 트리에서의 최솟값이 됩니다. 따라서 루트 노드의 오른쪽 서브트리에서 가장 작은 값을 가진 노드를 반환합니다.
그 다음 root 의 key 값에 오른쪽 서브 트리의 최솟값을 대입합니다. 이 과정이 루트 노드를 삭제하는 과정 중 key 를 삭제한 과정입니다.

그러나 key 값만 삭제한다고 끝난 것이 아니죠. 다시 루트 노드의 오른쪽에 있는 노드, 즉 오른쪽 서브트리에서 가장 작은 키 값을 가진 노드를 삭제합니다. 즉 30이라는 데이터를 삭제하고 싶으면 30 키 값을 가진 노드를 삭제하는 아이디어가 아닌, 오른쪽 서브 트리에서 가장 작은 값을 가진 노드(혹은 왼쪽 서브 트리에서 가장 큰 값을 가진 노드) 의 키 값을 복사하고, 그 노드를 해제함으로써 삭제 연산이 완료됩니다.
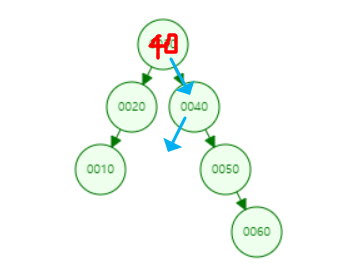
이 상태에서 왼쪽이 NULL 이므로 이 문제는 자식 노드가 한 개인 상황의 삭제로 변한 것이죠. 따라서 임시 temp 노드를 선언하고 temp 에 50을 가리키게 한 이후, 원조 40 키를 가진 노드를 해제한 이후 그 결과를 반환합니다. 그러면 그 시점이

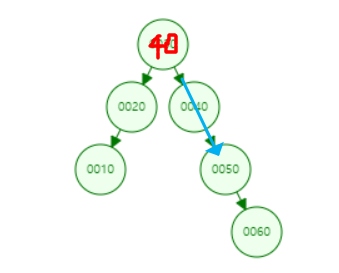
저 시점으로 돌아가게 되고, root 노드의 오른쪽에 50이 들어가면서 삭제가 완료되는 겁니다.
이진 탐색 트리 전체 코드 및 실행 결과
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode {
int key;
struct TreeNode* left, *right;
}TreeNode;
TreeNode* search(TreeNode* node, int key)
{
while (node != NULL) {
if (key == node->key) return node;
else if (key < node->key)
node = node->left;
else
node = node->right;
}
return NULL; // 탐색 실패인 경우 NULL 반환
}
TreeNode* new_node(int item)
{
TreeNode* ptr = (TreeNode*)malloc(sizeof(TreeNode));
ptr->key = item;
ptr->left = ptr->right = NULL;
return ptr;
}
TreeNode* insert_node(TreeNode* node, int key)
{
// 트리가 공백이면 새로운 노드 반환
if (node == NULL) return new_node(key);
// 그렇지 않다면 순환적으로 트리를 내려간다.
if (key == node->key) fprintf(stderr, "중복 key 값 오류\n");
else if (key > node->key)
node->left = insert_node(node->left, key);
else
node->right = insert_node(node->right, key);
// 변경된 루트 포인터를 반환
return node;
}
TreeNode* min_value_node(TreeNode* node)
{
TreeNode* current = node;
// 맨 왼쪽 단말 노드 탐색
while (current->left != NULL)
current = current->left;
return current;
}
TreeNode* delete_node(TreeNode* root, int key)
{
if (root == NULL) return root;
if (key < root->key)
root->left = delete_node(root->left, key);
else if (key > root->key)
root->right = delete_node(root->right, key);
else { // 키가 루트와 같다면 이 노드를 삭제
// 자식 노드가 0개 혹은 1개인 경우
if (root->left == NULL) {
TreeNode* temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL) {
TreeNode* temp = root->left;
free(root);
return temp;
}
// 자식 노드가 2개인 경우
TreeNode* temp = min_value_node(root->right); // 오른쪽 서브트리에서 가장 작은 값 탐색
// 중위 순회 시 후계 노드를 복사 (오른쪽 서브트리에서 가장 작은 값을 복사)
root->key = temp->key;
// 중위 순회 시 후계 노드를 삭제한다.
root->right = delete_node(root->right, temp->key);
}
return root;
}
void inorder(TreeNode* root) {
if (root) {
inorder(root->left);
printf("[%d] ", root->key);
inorder(root->right);
}
}
int main(void)
{
TreeNode* root = NULL;
TreeNode* tmp = NULL;
root = insert_node(root, 30);
root = insert_node(root, 20);
root = insert_node(root, 10);
root = insert_node(root, 40);
root = insert_node(root, 50);
root = insert_node(root, 60);
printf("이진 탐색 트리 중위 순회 결과\n\n");
inorder(root);
printf("\n\n");
if (search(root, 30) != NULL)
printf("이진 탐색 트리에서 30을 발견함\n");
else
printf("이진 탐색 트리에서 30을 발견 못함\n");
printf("\n\n");
delete_node(root, 30);
inorder(root);
printf("\n\n");
if (search(root, 30) != NULL)
printf("이진 탐색 트리에서 30을 발견함\n");
else
printf("이진 탐색 트리에서 30을 발견 못함\n");
return 0;
}
마지막으로 이진 탐색 트리의 삽입과 삭제 연산은 처음 접하면 생각보다 많이 헷갈립니다. 따라서 이를 시뮬레이션 할 수 있는 좋은 사이트를 공유하고자 합니다.
Binary Search Tree Visualization
www.cs.usfca.edu

위 홈페이지에서 삽입, 삭제, 탐색, 출력까지 단계별로 확인해볼 수 있으니 이진탐색트리가 익숙치 않다면 위 시뮬레이션 사이트에서 여러번 삽입과 삭제 등을 해보면서 익숙해지시면 됩니다. 감사합니다.

참고 :
https://code-lab1.tistory.com/10
C언어로 쉽게 풀어쓴 자료구조 - 생능출판
'C 자료구조' 카테고리의 다른 글
| [C 자료구조] 인접 리스트 그래프 탐색 ( DFS, BFS ) (0) | 2023.05.28 |
|---|---|
| [C 자료구조] 힙(Heap) - Max/Min heap (1) | 2023.05.27 |
| [C 자료구조] 스택을 이용한 트리 순회 (전위/중위/후위) (0) | 2023.05.25 |
| [C 자료구조 ] 트리의 순회(Traversal of Tree) - 전위 / 중위 / 후위 (1) | 2023.05.25 |
| [C 자료구조] 트리(Tree) 의 종류 (0) | 2023.05.25 |