힙(Heap) 이란?
힙(heap) 은 완전 이진 트리의 일종으로 여러 값들 중 최댓값 혹은 최솟값을 빠르게 찾아내기 위한 자료구조입니다.
이진 탐색 트리와는 다르게 힙은 중복된 값을 허용합니다. 완전 이진 트리는 지난 게시물에서 배웠었는데요 그 부분만 다시 보면
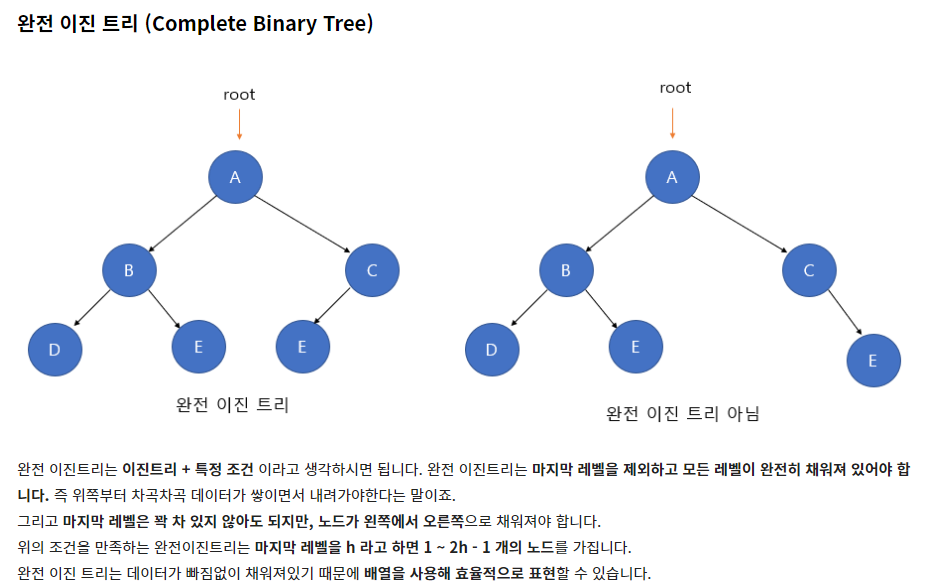
완전 이진 트리는 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져있고, 마지막 레벨은 왼쪽에서 오른쪽 순으로 데이터가 차 있는 이진 트리를 말합니다. Heap 은 중복 키 값을 허용하고, 부모 노드와 자식 노드 간의 관계가 정해져 있는 자료구조입니다.
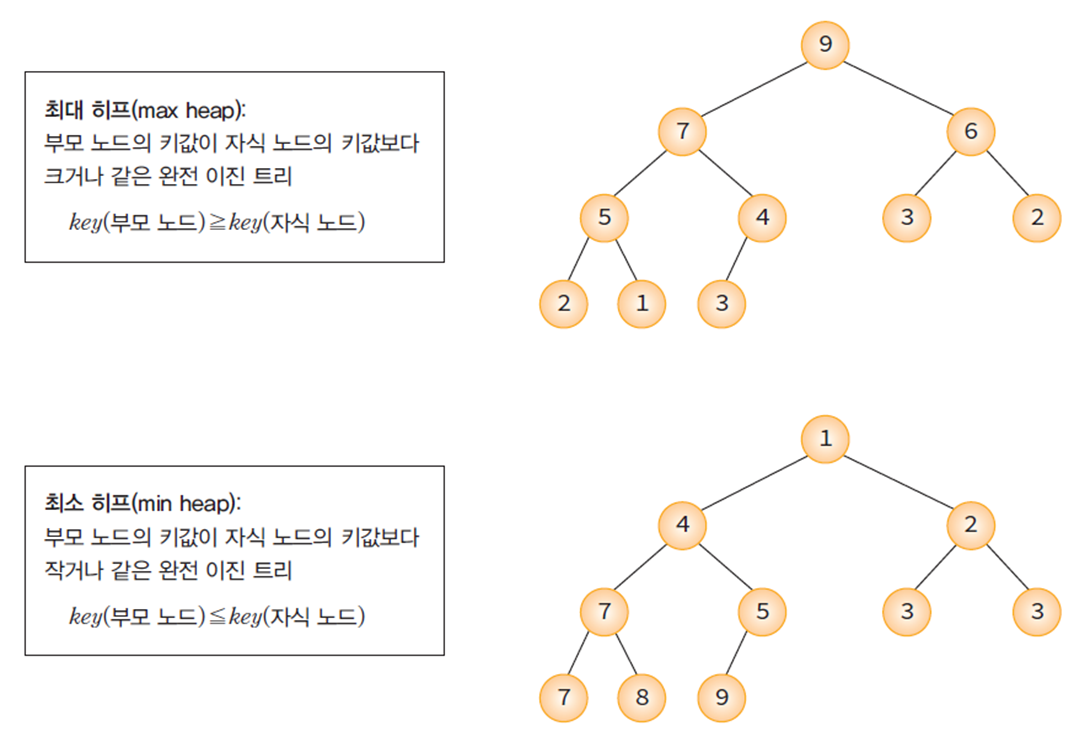
Max heap 와 Min heap 은 위처럼 부모 노드가 자식 노드보다 키값이 더 큰지 작은지로 결정됩니다. Max heap 은 가장 큰 값을 빠르게 찾을 수 있고, Min heap 은 가장 작은 값을 빠르게 찾을 수 있습니다.
최대 힙(Max heap) 은 key(부모 노드) ≥ key(자식 노드) 이고 최소 힙(Min heap)은 key(부모 노드) ≤ key(자식 노드) 의 구조로 이루어집니다.
이런 힙을 사용하는 가장 큰 이유는, 힙을 사용하게 되면 어떤 데이터의 삽입과 삭제에서 다른 자료구조로 구현할 때보다 더 낮은 시간복잡도로 수행할 수 있기 때문입니다.
| 표현 방법 | 삽 입 | 삭 제 |
| 순서없는 배열 | O(1) | O(n) |
| 순서없는 연결 리스트 | O(1) | O(n) |
| 정렬된 배열 | O(n) | O(1) |
| 정렬된 연결 리스트 | O(n) | O(1) |
| 힙 | O(logn) | O(logn) |
힙으로 된 구조에는 삽입과 삭제가 동일하게 logn 의 시간 복잡도로 수행됩니다. 따라서 평균적으로 가장 빠른 수행을 하게 되고 따라서 이를 통한 힙 정렬(Heap sort) 등은 다른 정렬들에 비해 빠른 속도를 가집니다. 힙은 완전 이진 트리이기 때문에 n개의 노드를 가지고 있는 힙의 높이는 O(log_2n) 이 됩니다. 아래에서 Heap 을 구현하면서 왜 정렬 연산이 O(logn) 의 시간 복잡도를 가지는지 확인해보겠습니다.
Heap 구현
Heap 은 완전 이진 트리이기 때문에 각각의 노드에 차례대로 번호를 붙일 수 있습니다. 따라서 힙은 배열을 통해 쉽게 구현할 수 있습니다. 완전 이진 트리는 배열에 저장하게 되면 연속된 인덱스를 통해 나타낼 수 있다는 특성이 있습니다.
[C 자료구조] 트리(Tree) 의 종류
트리(Tree) 란? 수학, 그래프 이론에서는 회로가 없는 무방향의 그래프를 트리라고 정의합니다. 이는 자료구조에서 쓰이는 트리와 기본적으로 같지만 차이가 좀 있습니다. 무슨 말인지 쉽게 알아
songsite123.tistory.com
왜 연속된 인덱스를 가지는가? 에 대한 내용은 위 포스팅에서 다루었으니 넘어가도록 하겠습니다.
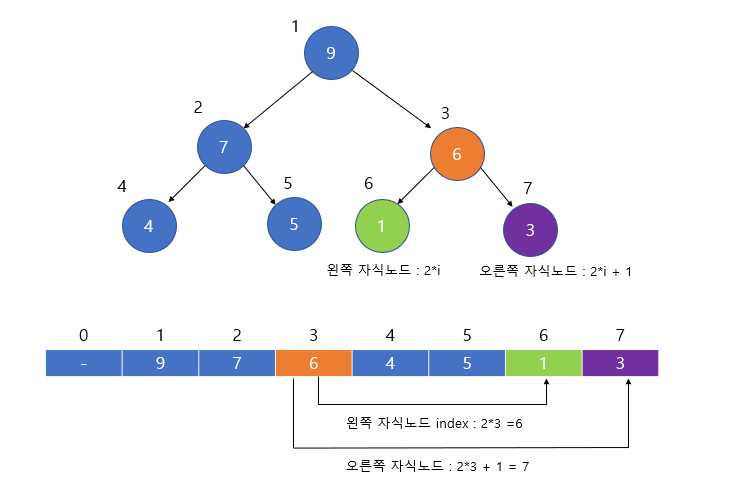
힙은 차례대로 번호를 붙여서 연속적으로 배열에 저장하게 되는데, 이 때 구현을 쉽게 하기 위해서 0 인덱스는 사용하지 않는 경우가 많습니다. 또한 배열을 이용해 히프를 저장하면 완전 이진 트리에서처럼 부모와 자식 노드를 쉽게 알 수 있습니다.
- 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = (자식의 인덱스) / 2
이제 힙을 정의하고, 이를 사용하기 위한 초기화 함수, 힙에 데이터를 넣는 삽입 연산과 데이터를 삭제하는 삭제 연산에 대해 알아보고 이를 코드로 구현해봅시다.
힙의 정의 / 초기화 함수
typedef struct {
int key;
}element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size;
}Heaptype;
Heaptype* create()
{
return (Heaptype*)malloc(sizeof(Heaptype));
}
void init(Heaptype* h)
{
h->heap_size = 0;
}먼저 key 값을 가진 element 구조체를 선언합니다. 이 때 element 에는 여러 가지 데이터 추가가 가능합니다. 예를 들어 학생의 학번, 이름, 성적을 묶어서 관리하고 싶으면 int key; 밑에 int num, char* name, int score; 이런 식으로 element 안에 추가해주면 됩니다.
그 다음으로 Heaptype 구조체를 선언합니다. Heap 은 스택과 유사하게 배열로 만들고 heap 안의 데이터가 몇 개인지를 알려주는 heap_size 변수도 선언해줍니다. 그 이후 create() 함수는 Heaytype 을 동적할당 받는 함수이고 init() 함수는 heap_size 를 0으로 초기화 시켜 줍니다. 선언이랑 생성, 초기화는 어려운 내용이 전혀 없습니다.
힙의 삽입 연산
힙의 삽입은 다음과 같은 과정을 거쳐서 수행됩니다.
- 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다. ( = 배열의 마지막에 원소를 추가한다. )
- 새로운 노드를 부모 노드와 비교해서 교환해야 한다면 힙의 성질을 만족할 때까지 교환한다.
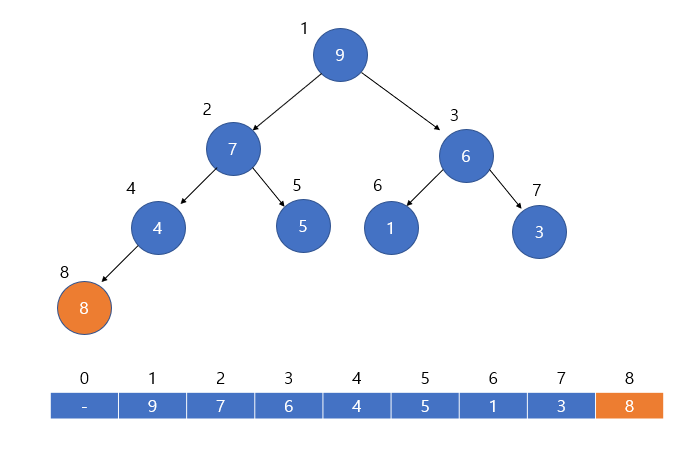
만약 8이라는 key 값을 가지는 element 를 삽입했다고 생각해봅시다. 가장 먼저 힙의 마지막 노드에 이를 붙입니다. 그 이후 부모 노드인 index 4번 노드와 키 값을 비교합니다. 그러면 이 구조는 heap 이 아니므로 8과 4는 위치를 교환합니다.
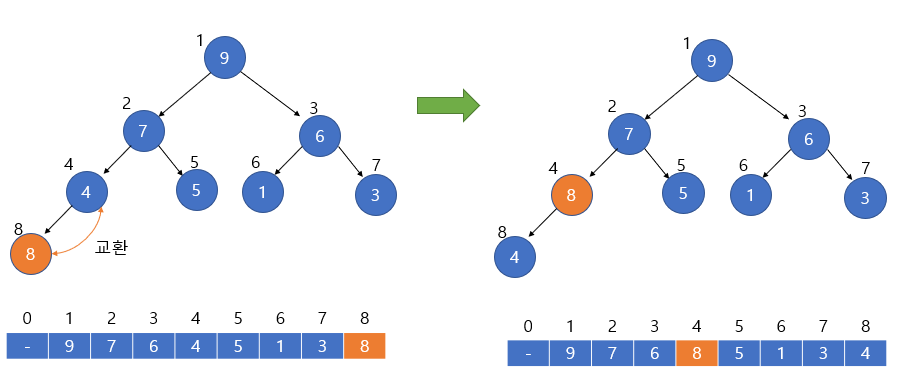
다시 8은 부모 노드인 7과 비교 연산을 진행합니다. 이번에도 8이 7보다 크기 때문에 서로 교환하는 연산이 수행됩니다.
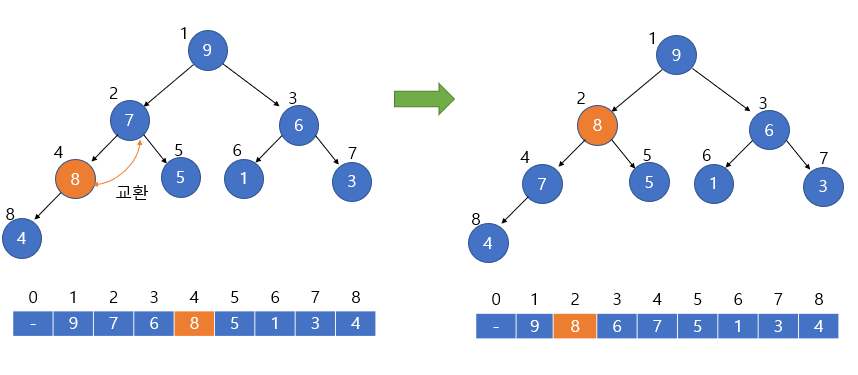
그 이후 8과 9를 비교하는 연산을 수행할텐데, 9는 8보다 크기 때문에 1번 인덱스와 2번 인덱스의 교환은 이루어지지 않고 삽입 연산이 종료됩니다.
이 알고리즘을 다시 단계별로 의사 코드로 살펴보면
- 히프 크기를 하나 증가시킨다.
- 증가된 히프 크기 위치에 새로운 노드 삽입
- i = heap_size
- i 가 루트 노드가 아니고 i번째 노드가 i의 부모 노드보다 크면
- i번째 노드와 부모 노드를 교환
void insert_maxheap(Heaptype* h, element item)
{
int i;
i = ++(h->heap_size);
// 트리를 거슬러 올라가며 부모 노드와 비교하는 과정
while ((i != 1) && (item.key > h->heap[i / 2].key)) {
h->heap[i] = h->heap[i / 2];
i /= 2;
}
h->heap[i] = item; // 새로운 노드를 삽입
}위에서는 자세한 이해를 위해 마지막 노드에 삽입한 후, 교환해간다고 설명했지만 실제로 배열로 구현한 힙에서 insert 연산을 함수로 구현하면 굳이 그럴 필요 없이 삽입할 노드를 아직 힙에 넣지 않고 손에 들고 있고 끝에서부터 비교하면서 맞는 위치에 삽입한다고 생각하시면 됩니다.
while 문을 통해 루트 노드까지 올라가거나 (최댓값) 혹은 부모 노드보다 작다면 while 문이 종료됩니다. heap 배열도 계속해서 덮어쓰고 i를 계속 절반 씩 바꿔가는 과정은 자식 노드의 값을 부모 노드에 넣는 과정을 말합니다. 삽입 연산의 시간 복잡도는 최대로 비교 연산을 수행해봤자 힙의 높이만큼의 연산만을 수행하게 됩니다. 그래서 삽입의 시간 복잡도가 O(logn) 으로 나오게 됩니다.
힙의 삭제 연산
Heap 에서의 삭제는 루트 노드를 삭제하고 반환합니다. 따라서 Heap 에서의 삭제는 다음 과정을 거칩니다. Maxheap 에서는 항상 최댓값이 루트 노드가 되기 때문에 어떤 값들을 힙에 삽입한 이후 그 만큼 삭제 연산을 수행하게 되면 그 자체로 오름차순 정렬된 결과를 출력하게 됩니다.
- 루트 노드를 삭제한다. (나중에 값을 반환해야 하므로 따로 저장)
- 삭제된 루트 노드의 위치에 힙의 가장 마지막 노드를 가져온다.
- 힙의 조건에 맞게 위치를 재설정한다. ( 이를 heapify 라고 한다. )

루트 노드를 삭제하고, 삭제된 루트 노드의 위치에 힙의 가장 마지막 노드를 가져옵니다.

힙의 조건에 맞게 위치를 재설정합니다. (heapify)
이 때 주의 해야할 점으로 비교할 노드보다 큰 자식 노드가 2개 있을 때, 더 큰 값을 가진 자식 노드와 교환해야 한다는 점입니다. 따라서 위 사진에서는 8과 6 중에서 8이 더 크므로 인덱스 2번으로 교환이 이루어집니다.
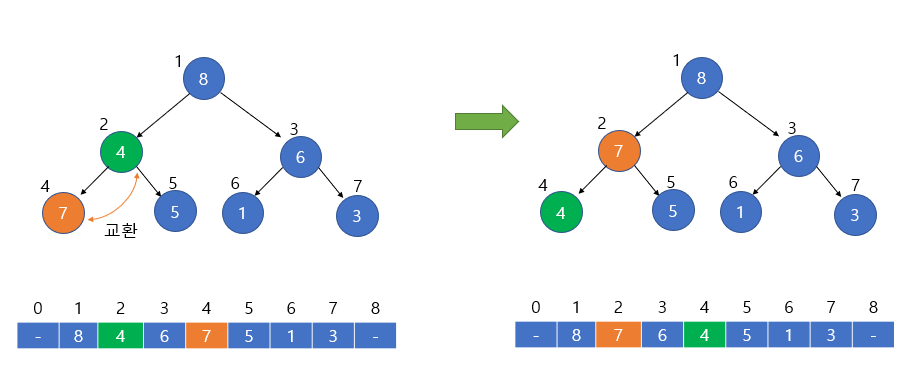
마찬가지로 힙의 조건에 맞게 위치를 재설정합니다. Max heap 의 조건을 만족하거나 단말 노드까지 내려가게 되면 반복이 종료되고 삭제 연산이 끝납니다.
element delete_maxheap(Heaptype* h)
{
int parent, child;
element item, temp;
item = h->heap[1];
temp = h->heap[(h->heap_size)--];
parent = 1;
child = 2;
while (child <= h->heap_size) {
// 현재 노드의 자식 노드 중 더 큰 자식 노드를 찾는다.
if ((child < h->heap_size) && (h->heap[child].key < h->heap[child + 1].key))
child++;
if (temp.key >= h->heap[child].key) break;
// 한 단계 아래로 이동
h->heap[parent] = h->heap[child];
parent = child;
child *= 2;
}
h->heap[parent] = temp;
return item;
}item 에는 heap 배열의 루트를 임시 저장합니다. 그리고 temp 에는 heap_size 의 값을 대입하고 heap_size 를 1 감소시킵니다. 가장 마지막 단의 노드를 빼고 이를 temp 에 저장한 것이고, 이제 이 temp 와 힙 내부를 위에서부터 비교연산하면서 넣을 자리를 찾아야 하는 것이죠.
자식 노드의 인덱스가 heap 사이즈보다 커지기 전까지 계속 반복합니다. 왼쪽과 오른쪽 중 만약 오른쪽이 더 크다면 인덱스를 1 증가시켜 오른쪽 서브트리를 선택하게 합니다. 아니라면 왼쪽으로 이동하게 되고 만약 넣을 자리를 찾는 다면, 종료하고 아니라면 한 단계 아래로 이동합니다. 이 때 아래로 이동하는 방법은 힙에서 부모 노드를 나타내는 parent 변수에 child 의 값을 대입하고, child 는 2를 곱한 값을 대입하는 겁니다. child 에 2를 곱하게 되면 무조건 짝수가 되기 때문에 왼쪽 자식 노드를 가리키게 됩니다. 이 상태에서 다시 whlie 문으로 돌아가서 만약 오른쪽이 더 크다면 1을 더해서 오른쪽을 선택하도록 만드는 것이죠.
반복문이 끝났다면 루트 노드를 꺼내고, 맨 아래 노드를 적절한 위치에 삽입합니다. 그리고 아까 복사해놨던 루트 노드값, 즉 item 을 반환합니다.
이 경우도 시간 복잡도는 O(logn) 이 최대 입니다. 힙의 높이 이상 비교연산이 이루어지지 않기 때문이죠. 이렇듯 힙에 삽입하고 꺼내기만 해도 그 결과값들을 나열하면 오름차순으로 정렬이 되는데 이를 사용한 정렬 방법이 힙 정렬 (Heap sort) 입니다.
전체 코드 및 실행 결과
#include <stdio.h>
#include <stdlib.h>
#define MAX_ELEMENT 100
typedef struct {
int key;
}element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size;
}Heaptype;
Heaptype* create()
{
return (Heaptype*)malloc(sizeof(Heaptype));
}
void init(Heaptype* h)
{
h->heap_size = 0;
}
void insert_maxheap(Heaptype* h, element item)
{
int i;
i = ++(h->heap_size);
// 트리를 거슬러 올라가며 부모 노드와 비교하는 과정
while ((i != 1) && (item.key > h->heap[i / 2].key)) {
h->heap[i] = h->heap[i / 2];
i /= 2;
}
h->heap[i] = item; // 새로운 노드를 삽입
}
element delete_maxheap(Heaptype* h)
{
int parent, child;
element item, temp;
item = h->heap[1];
temp = h->heap[(h->heap_size)--];
parent = 1;
child = 2;
while (child <= h->heap_size) {
// 현재 노드의 자식 노드 중 더 큰 자식 노드를 찾는다.
if ((child < h->heap_size) && (h->heap[child].key < h->heap[child + 1].key))
child++;
if (temp.key >= h->heap[child].key) break;
// 한 단계 아래로 이동
h->heap[parent] = h->heap[child];
parent = child;
child *= 2;
}
h->heap[parent] = temp;
return item;
}
int main(void) {
element e1 = { 10 }, e2 = { 5 }, e3 = { 30 };
element e4, e5, e6;
Heaptype* heap;
heap = create();
init(heap);
insert_maxheap(heap, e1);
insert_maxheap(heap, e2);
insert_maxheap(heap, e3);
e4 = delete_maxheap(heap);
printf("[%d] ", e4.key);
e5 = delete_maxheap(heap);
printf("[%d] ", e5.key);
e6 = delete_maxheap(heap);
printf("[%d] ", e6.key);
}
10, 5, 30 순으로 삽입하였으나 삭제 연산을 3번 진행하니 30, 10, 5 순으로 내림차순 정렬한 결과값이 나오게 됩니다. 이는 Maxheap 이기 때문에 그런 것이고 Minheap 에 같은 연산을 진행하면 오름차순으로 정렬한 값을 반환합니다. 그리고 이러한 힙은 우선순위큐 라는 자료구조를 만드는데 사용되기도 합니다. 감사합니다.

참고 및 출처 :
https://code-lab1.tistory.com/12
C언어로 쉽게 풀어쓴 자료구조 - 생능출판
'C 자료구조' 카테고리의 다른 글
| [C 자료구조] 인접 리스트 그래프 탐색 ( DFS, BFS ) (0) | 2023.05.28 |
|---|---|
| [C 자료구조] 이진 탐색 트리 (Binary Search Tree) (0) | 2023.05.25 |
| [C 자료구조] 스택을 이용한 트리 순회 (전위/중위/후위) (0) | 2023.05.25 |
| [C 자료구조 ] 트리의 순회(Traversal of Tree) - 전위 / 중위 / 후위 (1) | 2023.05.25 |
| [C 자료구조] 트리(Tree) 의 종류 (0) | 2023.05.25 |