아마 많은 프로그래밍을 배우는 학생들 중 행렬을 어떻게 저장하는가에 대한 고민을 안해본 사람도 있으실 것 같습니다. 파이썬에서 손 쉽게 행렬을 리스트나, 여러 자료구조로 다루지만 실제적으로 어떻게 저장해야 효율적인가? 는 이미 많이 최적화된 상태로 사용하고 있기 때문이죠.
그래도 행렬의 표현을 고민해보는 것은 자료구조를 이해하는데 있어 좋은 예제 중 하나입니다.
그 중에서도 희소 행렬(Sparse matrix)란 행렬의 원소 중에서 0인 값이 더 많은 행렬을 의미합니다. 이런 행렬은 추후 자연어처리 부분에서도 나타나기 때문에 어떻게 이를 안쓰고 효율적으로 모델링 할 수 있을까? 등 많이 고려되는 사항 중 하나입니다. 일반적으로 행렬은 $a[i][j]$ 와 같은 형태의 2차원 배열을 흔히 사용합니다. 그러나 Sparse matrix의 경우, 이 저장 구조가 적합하지 않습니다.
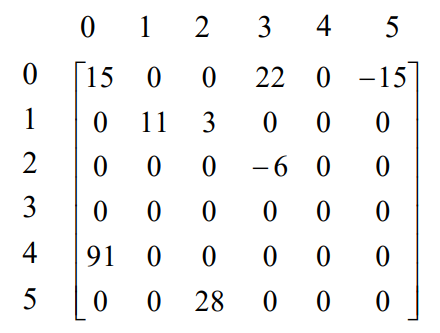
이 행렬은 36개의 저장공간을 사용하지만, 여기서 0이 아닌 항은 8개 밖에 안되고, 나머지 28개 공간은 0을 저장하고 있습니다. 지금은 예를 위해 6개라고 했지만, 실제로 사용하는 행렬이 $5000 \times 5000$ 이고, 그 중에서 5000개만 0이 아닌 원소를 가진다면 나머지 2천5백만 개의 메모리 공간이 낭비되기 때문입니다. 딥러닝을 공부하다보면 저 크기가 절대 과장이 아니라는 것을 알 수 있습니다.
따라서 이런 상황에는 0이 아닌 원소만 저장하는 표현법을 사용하면 시간과 공간을 많이 절약할 수 있습니다.
행렬은 3가지의 원소로 그 값을 저장할 수 있습니다. (row, col, value) 만 가지고 있으면 그 원소에 대한 위치 정보도 담고 있는 것이죠. 따라서 이전 포스팅의 다항식과 비슷한 아이디어로 전체 행렬을 나타내는 클래스인 SparseMatrix 클래스가 있고, friend 클래스로 각 행렬의 항을 저장하는 MatrixTerm 클래스를 선언하여 사용할 수 있습니다. 연산의 구현은 덧셈, 곱셈, 전치만 구현하도록 SparseMatrix와 MatrixTerm의 ADT를 구상해보면 다음과 같습니다.
#ifndef SPARSEMATRIX_H
#define SPARSEMATRIX_H
class SparseMatrix {
public:
SparseMatrix();
~SparseMatrix();
SparseMatrix Transpose();
SparseMatrix Add(SparseMatrix b);
SparseMatrix Multiply(SparseMatrix b);
private:
int rows, cols, terms, capacity;
MatrixTerm* smArray;
friend ostream& operator<<(ostream&, SparseMatrix&);
friend istream& operator>>(istream&, SparseMatrix&);
};
class MatrixTerm {
friend class SparseMatrix;
private:
int row, col, value;
};
#endif이 때 SparseMatrix 내의 rows 는 행렬의 행의 수, cols는 행렬의 열의 수, terms 는 0이 아닌 항의 총 개수, capacity는 확보한 smArray의 크기를 의미합니다. 위 방식으로 예시 행렬을 저장하면 오른쪽 그림과 같이 저장됩니다.

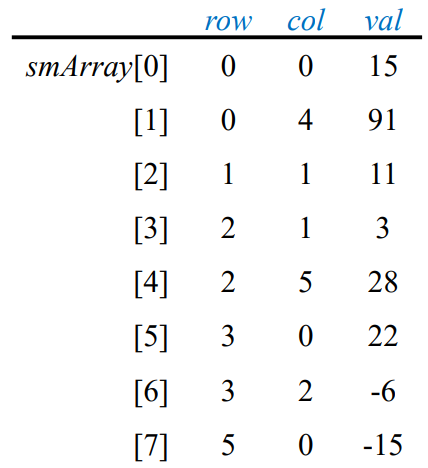
이 경우 rows = 6, cols = 6, terms = 8, capacity는 8 이상이 되겠죠?
덧셈은 배열로 표현한 다항식의 구현 코드와 매우 유사해서 생략하도록 하겠습니다. 우선 행렬의 덧셈은 차원이 같아야 정의되기 때문에 2개의 행렬에 대해 차원이 같은지 체크하고 같다면 각 원소별로 element-wise 덧셈을 수행하게 됩니다. 차원이 같아도 두 행렬이 가지는 Term의 개수는 다를 수 있기 때문에 배열 다항식 표현에서 사용했던 덧셈의 아이디어가 동일하게 사용됩니다. 행이 먼저 오름차순으로 정렬되고 그 이후 열이 오름차순으로 정렬된다는 것을 이용해 증가시키면서 둘 다 같은 위치에 값이 존재한다면 value를 더하여 새로운 SparstMatix에 추가하고, 하나만 있다면 그 값만 새로운 matrix에 추가하는 방식으로 동작합니다.
행렬만의 연산인 전치(Transpose)와 행렬의 곱셈 메커니즘에 대해 설명해보고 간단한 pseudo-code 만 보고 마무리하도록 하겠습니다.
원래 기본적인 행렬 저장 방법인 2차원 배열로 구현하는 경우 행렬의 전치는 매우 직관적이고 간단합니다. $(i,j) \to (j,i)$ 라는 연산을 취해서 만들면 되기 때문입니다.
for(int i = 0; i <cols; i++)
for(int j = 0; j< rows; j++)
b[j][i] = a[j][i];아주 단순한 알고리즘으로 행렬의 전치를 구할 수 있습니다. 그러나 이 경우 시간복잡도를 생각해보면 $O(rows\times cols)$ 의 시간이 걸리게 됩니다. 정방행렬이라면 $O(n^2)$의 시간 복잡도를 가지게 됩니다.
그런데 우리는 무엇보다 위 방법처럼 2차원 배열로 지금 행렬을 표현하고 있지 않습니다. 따라서 다른 전치 함수가 필요합니다.
SparseMatrix SparseMatrix::Transpose()
{ // *this의 전치 행렬을 반환
SparseMatrix b(cols, rows, terms); // b.smArray의 크기는 terms
if (terms > 0)
{ // 0이 아닌 행렬
int currentB = 0;
for (int c = 0; c < cols; c++) { // 열별로 전치
for (int i = 0; i < terms; i++) {
// 열 c로부터 원소를 찾아 이동
if (smArray[i].col == c) {
b.smArray[currentB].row = c;
b.smArray[currentB].col = smArray[i].row;
b.smArray[currentB].value = smArray[i].value;
}
}
}
}
return b;
}위 프로그램은 위에서 정의한 희소행렬의 형태로 저장한 경우 Transpose를 하는 함수입니다. 그러나 위 알고리즘의 시간 복잡도는 $O(terms\cdot cols)$가 되는데, 만약 희소행렬이 아니여서 terms의 크기가 $cols \times rows$가 되는 경우 거의 $O(n^3)$ 정도까지 될 수 있는 매우 느린 알고리즘이죠. 위에 써 놓은 3줄짜리 코드보다도 시간 복잡도가 나쁩니다.
SparseMatrix SparseMatrix::FastTranspose()
{// *this의 전치를 O(terms + cols) 시간에 반환한다.
SparseMatrix b(cols, rows, terms);
if (terms > 0)
{// 0이 아닌 행렬
int* rowSize = new int[cols];
int* rowStart = new int[cols];
// compute rowSize[i] = b의 행 i에 있는 항의 수를 계산
fill(rowSize, rowSize + cols, 0); // 초기화
for (i = 0; i < terms; i++) rowSize[smArray[i].col]++;
// rowStart[i] = b의 행 i의 시작점
rowStart = 0;
for (i = 1; i < cols; i++) rowStart[i] = rowStart[i - 1] + rowSize[i - 1];
for (i = 0; i < terms; i++)
{// *this를 b로 복사
int j = rowStart[smArray[i].col];
b.smArray[j].row = smArray[i].col;
b.smArray[j].col = smArray[i].row;
b.smArray[j].value = smArray[i].value;
rowStart[smArray[i].col]++;
} // for의 끝
delete[] rowSize;
delete[] rowStart;
} // if의 끝
return b;
}위 코드는 메모리를 조금 더 사용하지만 속도는 개선한 FastTranspose 알고리즘입니다.
- 먼저 행렬 *this의 각 열에 대한 원소 수를 구하고
- 전치 행렬 b의 각 행의 원소수(= 행렬 a의 각 열의 원소수)를 결정
- 이 정보를 통해 전치행렬 b의 각 행의 시작 위치를 구하고
- 원래 행렬 a에 있는 원소를 하나씩 전치 행렬의 b의 위치로 옮깁니다.
이 알고리즘의 시간 복잡도는 $O(cols+terms)$ 로 이전에 비해 매우 빨라진 알고리즘입니다.
Reference : Ellis, Horowitz. C++ 자료구조론(2판). 대한민국: 인피니티북스, 2007.
'C++ > C++ 자료구조' 카테고리의 다른 글
| BFS 를 사용해 미로의 최단 경로 출력하기 (1) | 2023.10.15 |
|---|---|
| Container class - Bag, Stack, Queue C++ pesudo code (1) | 2023.10.15 |
| 배열을 이용한 다항식 ADT의 표현 (Polynomial ADT using Array) - 다항식의 덧셈과 곱셈 (0) | 2023.10.15 |
| [C++] STL 정리 ( pair, vector, stack, queue, deque, map, set, algorithm ) (0) | 2023.05.05 |