컨테이너 클래스(Container class)란 다수의 데이터 객체들을 수용 또는 저장하는 자료 구조를 표현하는 클래스 를 말합니다. 컨테이너 클래스는 일반적으로 객체들을 삽입하거나 삭제할 수 있으며, 앞에서 보았던 배열도 컨테이너 클래스의 일종입니다. 앞으로 여러 형태의 컨테이너 클래스들을 보게 될텐데, 오늘은 C++ pesudo code 를 위주로 Bag, Stack, Queue 를 확인해보도록 하겠습니다. 각 개념에 대한 설명은 C 자료구조에서 자세히 해놨기 때문에 링크만 걸고 코드 위주로 보겠습니다.
Bag 클래스란 이름 그대로 가방입니다. 삽입(Push)하고, 삭제(Pop)하고, 비었는지 확인하고(IsEmpty), 안에 몇 개가 들어가 있는지를 확인(Size)하는 기능이 담겨 있습니다.
템플릿 클래스를 이용해 Bag을 선언한 코드는 아래와 같습니다.
template <class T>
void ChangeSize1D(T*& a, const int oldSize, const int newSize)
{
if (newSize < 0) throw “New length must be >= 0”;
T* temp = new T[newSize]; // new array
int number = min(oldSize, newSize);
copy(a, a + number, temp);
delete[] a;
a = temp;
}
template <class T>
class Bag
{
public:
Bag(int bagCapacity = 10);
~Bag();
int Size() const { return top + 1; }
bool IsEmpty() const { return size == 0; }
void Push(const T&);
void Pop();
private:
T* array; // 배열
int capacity; // 배열의 크기
int top; // top 원소의 배열 위치
};
template <class T>
Bag<T>::Bag(int bagCapacity) : capacity(bagCapacity) {
if (capacity) < 1 throw "Capacity must be > 0"
array = new T[capacity];
top = -1;
}
template <class T>
Bag<T>::~Bag() { delete[] array; }
template <class T>
void Bag<T>::Push(const T& x) {
if (capacity == top + 1) {
ChangeSize1D(array, capacity, 2 * capacity);
capacity *= 2;
}
array[++top] = x;
}
template <class T>
void Bag<T>::Pop() {
if (IsEmpty()) throw "Bag is empty";
int deletePos = top / 2;
copy(array + deletePos + 1, array + top + 1, array + deletePos);
top--;
}사실 Bag 자료구조는 전혀 쓰이지 않고, 스택의 틀을 잡아놓은 기본 자료구조라고 생각하시면 됩니다. 스택과 겹치게 되므로 따로 설명은 하지 않고 넘어가도록 하겠습니다.
[C 자료구조] 스택(Stack)
스택(Stack)이란? 스택(Stack)은 자료구조의 한 종류입니다. 두 개의 포인터로 많은 양의 데이터를 관리하는 이론? 구조? 이죠. 자료구조 중에서 '선형구조'에 해당하는 자료구조인데요, 어려울 거
songsite123.tistory.com
위 포스팅에 스택이 무엇이고 무슨 특징을 가지는지에 대해 다루고 C언어로 기초 코드를 구현해놓았습니다. 스택은 정말 자주 사용되는 자료구조이죠. 스택은 LIFO 라는 특징을 가집니다. C++에서는 위 포스팅에서 구현한 함수들까지 싹 모아서 하나의 클래스로 만들어서 템플릿으로 구현합니다. 실제로 추후에 사용할 때는 #include <stack> 이나 #include <vector> 를 통해 만들어진 STL 클래스를 사용하면 됩니다.
template <class T>
class Stack {
Stack(int capacity = 10);
bool IsEmpty() const;
T& Top() const;
void Push(const T& x);
void Pop();
private:
T* stack; // 스택 원소를 위한 배열
int top; // 톱 원소의 위치
int capacity; // 스택 배열의 크기
template <class T>
Stack<T>::Stack(int stackCapacity) : capacity(stackCapacity)
{
if (capacity < 1) throw “Stack capacity must be > 0”;
stack = new T[capacity];
top = -1;
}
};
template <class T>
Stack<T>::Stack(int stackCapacity) :capacity(stackCapacity) {
if (capacity < 1) throw "Stack capacity must be > 0";
stack = new T[capacity];
top = -1;
}
template <class T>
inline bool Stack<T>::IsEmpty() const { return top == -1; }
template <class T>
inline T& Stack<T>::Top() const {
if (IsEmpty()) throw “Stack is empty”;
return stack[top];
}
template <class T>
void Stack<T>::Push(const T& x) { // Add x to the stack
if (top == capacity – 1) {
ChangeSize1D(stack, capacity, 2 * capacity);
capacity *= 2;
}
stack[++top] = x;
}
template <class T>
void Stack<T>::Pop() { // Delete top element from the stack.
if (IsEmpty()) throw “Stack is empty.Cannot delete.”;
stack[top--].~T(); // destructor for T
}1차원 배열을 이용한 기본적인 구조의 Stack 클래스입니다.
[C 자료구조] 큐(Queue) - 선형큐 / 원형큐 배열 구현
큐(Queue) 란? 스택의 경우, 나중에 들어온 데이터가 먼저 나가는 LIFO 구조인 반면, 큐(Queue) 는 먼저 들어온 데이터가 먼저 나가는 자료구조입니다. 이런 특성을 FIFO (First-In First-Out) 이라고 합니다.
songsite123.tistory.com
다음으로 FIFO의 특징을 가지고 있는 자료구조인 큐(Queue)입니다. 한쪽 끝에서 삽입이 일어나고 그 반대쪽 끝에서 삭제가 일어나는 순서 리스트입니다. 원소가 삽입되는 끝이 rear, 원소가 삭제되는 끝을 front 라고 합니다. 이번 포스팅에서 다루는 큐의 구현은 배열을 통해 구현합니다. 그러나 큐 같은 경우는 배열로 구현하기엔 비효율적인 구조 입니다.
배열로 큐를 구현하는 경우, 원소를 삽입할 때의 시간 복잡도는 O(1)이지만 삭제할 때는 queue[0]에 있는 앞 원소를 제거할 때마다 나머지 원소들을 왼쪽으로 이동해야 하기 때문에 O(n)의 시간 복잡도를 가지기 때문입니다.
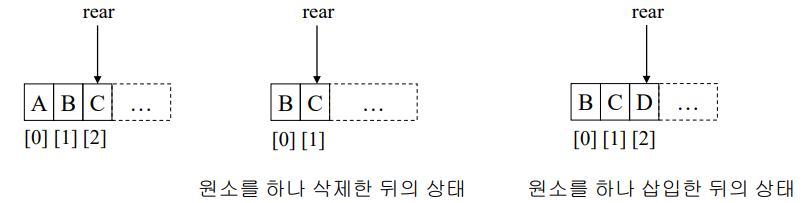
이러한 현상이 발생하는 이유는 queue[0]에 항상 원소가 채워져 있어야 한다는 제약을 걸어서 그렇습니다. 굳이 배열 처음부터 차곡차곡 안 쌓고, 중간에만 채워져 있으면 안돼? 라는 아이디어로 front를 0이 아닌 front 변수를 사용해 나타내게 된다면 삭제할 때도 시간 복잡도가 O(1) 이 됩니다.
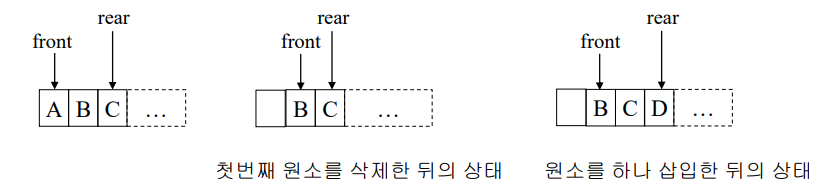
그러나 이런 구조를 사용하면 rear가 capacity-1 과 같게 되어서 맨 오른쪽으로 가버리면 앞쪽에 자리가 있음에도 불구하고 더 삽입할 수 없다는 메모리 낭비가 발생합니다.
이러한 현상을 해결하기 위해 큐가 배열의 끝에서 다시 되돌아오게 만든다면 삭제와 삽입 시간이 모두 O(1)인 큐를 만들 수 있습니다. 이러한 형태의 큐를 원형큐(circular queue) 라고 합니다.
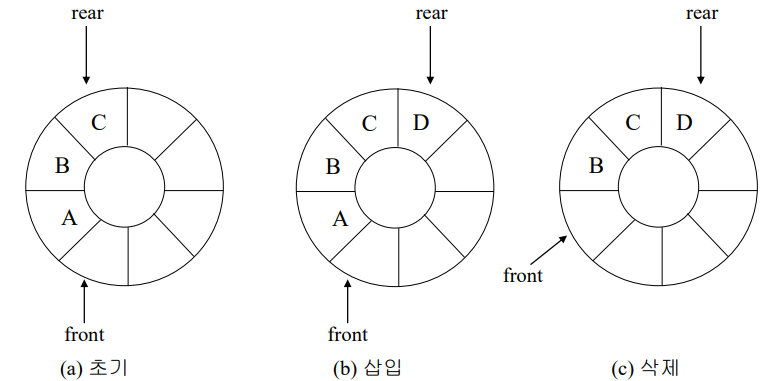
이러한 구조의 문제점은 front = rear 인 경우에 대해 큐가 꽉 차있는건지, 다 비어있는건지 구분할 방법이 없다는 사실입니다. 따라서 한 칸의 공간을 사용하지 않기를 사용하면 front와 rear가 같은 경우오직 비어있는 경우를 뜻하고, front와 rear가 1만큼 차이가 난다면 (capacity보다 커질 수 있는 값에 대해 % capacity를 적용한 값에 대한 차)가 1인 경우에만 큐가 꽉 차있다고 간주합니다.
이 아이디어를 통해 Push 에서도 큐가 꽉 차있다는 조건을 if ((rear + 1) % capacity == front) 로 사용합니다. rear를 한 칸 증가시키고 넣으려고 봤더니 front랑 똑같다 = 큐가 꽉 차있으니 크기를 2배로 늘리자는 방식으로 구현합니다.
template <class T>
class Queue {
Queue(int queueCapacity = 8);
bool IsEmpty();
T& Front();
T& Rear();
void Push(const& x);
void Pop();
private:
T* queue; // 큐 원소들을 저장한 배열(heap영역에 위치)
int front, // 첫번째 원소의 위치 직전 위치
rear, // 마지막 원소의 위치
capacity; // 현재 확보된 큐 배열의 크기
};
template <class T>
Queue<T>::Queue(int queueCapacity) : capacity(queueCapacity)
{
if (capacity < 1) throw “Queue capacity must be > 0”;
queue = new T[capacity];
front = rear = 0;
}
template <class T>
inline bool Queue<T>::IsEmpty() { return front == rear; }
template <class T>
inline T& Queue<T>::Front() {
if (IsEmpty()) throw “Queue is empty.No front element”;
return queue[(front + 1) % capacity];
}
template <class T>
inline T& Queue<T>::Rear() {
if (IsEmpty()) throw “Queue is empty.No rear element”;
return queue[rear];
}
template <class T>
void Queue<T>::Push(const& x)
{// add x at rear of queue.
if ((rear + 1) % capacity == front)
{//queue full, double capacity:queue capacity 2
T* newQueue = new T[2 * capacity];
int start = (front + 1) % capacity;
if (start < 2) // no wrap around
// 빈 칸이 0이나 1 인덱스에 존재하는 경우, 배열의 오른쪽 끝까지만 원소가 차있음
copy(queue + start, queue + start + capacity- 1, newQueue);
// copy from queue to new Queue
else {
// 아닌 경우 오른쪽에 있는걸 먼저 복사한다음에, 처음부터 rear까지 복사해야한다.
copy(queue + start, queue + capacity, newQueue);
copy(queue, queue + rear + 1, newQueue + capacity - start);
}
// switch to newQueue
front = 2 * capacity– 1; rear = capacity - 2; capacity *= 2;
delete[] queue;
queue = newQueue;
}
rear = (rear + 1) % capacity;
queue[rear] = x;
}
template <class T>
void Queue<T>::Pop() {
if (IsEmpty) throw "Queue Empty";
front = (front + 1) % capacity;
}Push의 구현만 조금 더 설명하자면 2배를 확장 시키는 건 새로운 큐를 만들어 원래의 큐를 카피해서 반환하는 방식을 사용합니다. 그러나 이 때 원형 큐인 경우에 오른쪽에만 데이터가 차 있는 경우에는 한 번의 copy로 해결이 되지만, 오른쪽과 왼쪽에 모두 데이터가 있는 경우 front에서 배열의 끝가지 먼저 copy를 한 이후에 처음부터 rear까지 복사를해야 합니다. 2번째 복사에서의 위치는 앞서 복사한 다음 위치가 되어야 하므로 첫번째 Copy에서 newQueue부터 Queue + capacity - start - 1 까지 복사가 되기 때문에 그 위치를 기점으로 왼쪽에서 복사한 것을 붙여넣는 방식입니다.
그런데 저 남은 한칸을 사용하면 안되냐? 라고 물어볼 수 있는데 이는 lastOP 변수, 즉 마지막 연산이 Push였는지 Pop이였는지를 기억하는 변수를 만들게 되면 모든 저장 공간을 사용할 수 있습니다. 그러나 이 방식을 사용하면 삽입, 삭제 연산이 느려지고, 큐는 삽입 삭제가 빈번히 일어나는 자료구조이기 때문에 일반적으로 한 칸을 빼놓고 구현하는 것이 더 유리합니다.
Reference : Ellis, Horowitz. C++ 자료구조론(2판). 대한민국: 인피니티북스, 2007.
'C++ > C++ 자료구조' 카테고리의 다른 글
| BFS 를 사용해 미로의 최단 경로 출력하기 (1) | 2023.10.15 |
|---|---|
| 배열을 이용한 희소 행렬 표현 (Sparse matrices representations using Array) (1) | 2023.10.15 |
| 배열을 이용한 다항식 ADT의 표현 (Polynomial ADT using Array) - 다항식의 덧셈과 곱셈 (0) | 2023.10.15 |
| [C++] STL 정리 ( pair, vector, stack, queue, deque, map, set, algorithm ) (0) | 2023.05.05 |