Towards Deep Learning Models Resistant to Adversarial Attacks (ICLR 2018) - PGD Attack

인공지능 보안 분야에서 정말 유명한 논문인 PGD Training 에 관한 논문입니다. Adversarial attacks 에 대한 Defense 쪽에서는 현재 나오는 논문에서도 베이스라인으로 많이 비교하고 인용 횟수가 1만에 가까운 논문이죠. PGD Attack 을 활용해 robust 한 신경망을 얻어내는 과정과 그 결과물에 대해 배포한 논문입니다. 그럼 논문을 읽어보며 PGD attack이란 도대체 무엇인지, 이걸 통해 어떻게 방어 성능이 좋은 모델을 만들어냈는지 확인해보도록 하겠습니다.

 

---

Abstract

최근의 연구들은 심층 신경망이 일반 데이터와 거의 구별할 수 없는 adversarial examples들에 매우 취약하다는 것을 보여주었습니다. 이전 논문 리뷰인 FGSM 에서도 다루었죠. 이후의 연구들에서도 adversarial attacks의 존재가 곧 딥러닝 모델의 취약점이 된다는 것을 보여줍니다. 이 문제를 해결하기 위해 본 논문에서는 신경망의 adversarial robustness(적대적 공격에 대한 저항성 정도로 이해하시면 될 것 같습니다.)를 얻기 위해 최적화에 대한 측면에서 이를 분석합니다.

이 접근법은 이 주제에 대한 대부분의 이전 연구에 대해 광범위하고 통일적인 견해를 제공합니다. 특히, 어떤 adversarial attack이 와도 정상적으로 잘 동작할 수 있도록 구체적으로 보장하는 메서드에 중점을 두었습니다. 이런 메서드을 통해 adversarial attack에 대한 저항력이 크게 향상된 네트워크를 훈련시킬 수 있습니다. 논문에서 PGD attack을 통해 PGD Training을 시키는데, 이는 first-order attack의 일종입니다. 이 공격을 통해 만들어진 adversarial example를 사용하여 다시 학습을 진행하면 다른 first-order attack 에 대해서도 저항성을 보장할 수 있고, 이는 앞으로 지향해야하는 완전히 저항적인, 즉 adversial attack을 완전히 막을 수 있는 딥러닝 모델을 향한 중요한 step이 될 것이라 주장합니다.

 

 

1. Introduction

CV와 NLP 같은 분야의 훈련된 모델들은 benign한 input, 즉 일반적인 input에 대해서는 아주 높은 정확도를 보이지만, adversarially chosen input, 의도적으로 생성한 adversarial example 같은 input에 대해서는 잘못된 결과값을 도출해냅니다. 이를 방어하기 위한 방법을 고려한 설계는 하나의 중요한 목표가 되어가고 있습니다. 본 논문에서는 어떻게 심층 신경망을 adversarial input에 대해 저항할 수 있게 만드는가? 에 대해 다룹니다. ( How can we train deep neural networks that are robust to adversarial inputs? )

 

이 논문 이전에도 여러 공격과 방어 기법에 대해 다양한 방법이 제시되었습니다. 하지만 그 방법들이 가장 강력한 공격이라고 보장할 수 없고, 반대로 가장 효과적인 방어법이라고 보장할 수도 없습니다. 이 논문 이전에도 adversarial input 에 대한 다양한 방어 기법과 그 모델에 대해 공격하는 과정이 많이 반복되었는데, 이전의 defense 기법들은 실질적으로 방어가 되나 싶다가도 좀 더 강력한 공격이 들어오면 뚫리거나 시간이 너무 오래 걸리거나 하는 연구가 많았고, 논문에서는 그러한 이전 연구의 특성과 한계점들에 대해 간략히 설명합니다. 이 논문 같은 경우는 강력한 공격에 대해서도 robust 한, 방어가 되는 사실상 최초의 방어 기법을 제안합니다.

 

본 논문에서는 신경망의 adversarial robustness를 robust optimization의 측면에서 봅니다. saddle point(min-max) formulation을 이용해 보안성을 보장할 수 있으며 이 formulation을 통해 공격과 방어 모두를 수행할 수 있습니다. 특히 adversarial training을 통해 가장 최적인 saddle point를 찾아 다른 공격에 대해서도 robust 한 모델을 만들 수 있다고 주장합니다. 이러한 관점에서 본 논문은 다음과 같은 contribution을 가집니다.

1. First-order method 중 PGD attack을 통해 saddle point formulation에 최적화 될 수 있는 모델을 만드는 법을 제시합니다. (강력한 공격 기법들에 대해 robust 한 신경망을 만들었음)
2. 아키텍처가 adversarial robustness에 미치는 영향을 연구하여 모델 용량, 모델의 capacity 가 중요하다는 사실을 알아냈습니다. Adversarial robustness 를 위해서는 capacity가 큰 모델이 필요하다는 것을 입증합니다.
3. MNIST와 CIFAR-10 데이터에 대해 PGD training 을 사용해 robust한 모델을 만들고 배포했습니다. 뿐만 아니라 배포한 모델을 뚫어보라고 대회까지 열어서 정말 다양한 공격 기법에 대해서 탁월한 방어 성능을 가지고 있음 또한 입증해냅니다. 

실제 챌린지에 대한 주소는 https://github.com/MadryLab/mnist_challenge에서 확인할 수 있습니다.

GitHub - MadryLab/mnist_challenge: A challenge to explore adversarial robustness of neural networks on MNIST.

(CIFAR-10 challenge : https://github.com/MadryLab/cifar10_challenge )

GitHub - MadryLab/cifar10_challenge: A challenge to explore adversarial robustness of neural networks on CIFAR10.

 

 

2. An Optimization View on Adversarial Robustness

앞으로의 논의는 adversarial robustness를 최적화하는 관점을 중심으로 전개됩니다. 이 관점은 연구하고자 하는 현상을 정확히 나타낼 뿐 아니라, 앞으로의 방향성 또한 제시해줍니다. 이를 위해 표준적인 분류 task를 고려하겠습니다.

 

기본적인 데이터 분포 $\mathcal{D}$에 대한 입력 $x\in \mathbb{R}^d$과 대응되는 라벨 $y \in [k]$가 있습니다. 이에 대한 적합한 loss function(ex. cross entropy)을 $L(\theta, x, y)$로 기술하고 이 때 $\theta \in \mathbb{R}^p$는 모델의 파라미터를 뜻합니다. 목표는 risk인 $\mathbb{E}_{(x, y)~ \mathcal{D}}[L(x, y, \theta)]$를 최소화 시킬 수 있는 $\theta$를 찾는 것입니다. 일반적인 신경망이 loss 값을 계산하여 loss값을 줄이는 방향으로 학습하는 것을 말하는 겁니다. 그 중 Emprical risk minimization(ERM) 도 train error를 최소화 시키는 한 가지 방법입니다. 그러나 ERM은 모든 adversarial example에 대해 robust하지 않습니다. adversarial attack 중에서 $c_1$ 이라는 클래스를 가지는 $x$라는 입력 데이터를 아주 근처에 있는 $c_2$ 클래스를 가지는 $x^{adv}$라는 입력처럼 바꾸는 방식의 공격이 있습니다. 모델은 이런 데이터에 대해 클래스를 잘못 분류하여 분명 클래스가 다른, $c_2 \neq c_1$임에도 불구하고 $c_1$ 데이터를 $c_2$ 클래스로 분류합니다.

 

위 같은 케이스도 막아낼 수 있는 Adversarial attacks에 강한 모델을 안정적으로(reliably) 훈련시키기 위해서는 ERM 패러다임을 적절히 확대할 필요가 있습니다. 본 논문의 접근법은 특정 공격에 대한 robustness 향상에 직접적으로 초첨을 맞추는 방법 대신 adversarially robust한 모델이 충족해야하는 guarantee 를 제시하는 것입니다.

 

첫 번째 단계는 모델이 방어해야하는 attack model에 대한 명확한 정의를 하는 것입니다. 각 데이터 포인트 $x$에 대해 공격 모델의 성능을 공식화 할 수 있도록 perturbation $\mathcal{S} \in \mathbb{R}^d$를 정의합니다. 이미지 분류 task에서는 $\mathcal{S}$를 선택함으로써 이미지 간의 지각적 유사성(perceptual similarity)를 포착합니다. 예를 들어 $l_∞ $-ball around $x$는 최근의 연구에서 adversarial perturbation에 대한 자연스러운 개념으로 연구되었습니다. [ 이전 연구 논문 리뷰 ] 본 논문에서는 $ l_∞$-bounded attacks 에 대한 robustness에 초점을 맞춥니다.

 

다음으로 위의 adversary를 포함하여 rist $\mathbb{E}_{\mathcal{D}}[L]$에 대한 정의를 수정합니다. 분포 $\mathcal{D}$의 sample들이 loss $L$로 직접 반영되는 것이 아닌, adversary가 먼저 입력을 교란 시킬 수 있도록 허용합니다. (Instead of feeding samples from the distribution $\mathcal{D}$ directly into the loss $L$, we allow the adversary to perturb the input first.) 이는 본 논문의 핵심 주제인 saddle point problem 을 제시해줍니다.

 

$$ \min_{\theta} \rho(\theta),  \quad \text{where} \quad \rho(\theta) = \mathbb{E}_{(x,y) ~ \mathcal{D}} \left[\max_{\gamma \in \mathcal{S}} L(\theta, x + \gamma, y) \right] $$

 

이런 형태는 최적화 이론에서 유명한 형태이며, loss $L$을 최대로 만드는 adversarial 에 대한 loss $L$의 값이 최소가 되도록 학습을 시킨다는 의미입니다. 

 

이 수식은 이전의 adversarial robustness의 연구에 대한 통합적인 관점을 제시합니다. 본 논문의 관점은 안장점 문제를 내부 최대화 문제와 외부 최소화 문제의 구성으로 보는 것에서 비롯됩니다. 

• inner maximazation problem : 주어진 데이터 $x$가 가장 높은 loss를 얻는 adversarial version 을 찾는 것
• outer minimization problem : inner attack problem에 의해 주어진 adversarial loss가 최소화될 수 있는 모델 파라미터를 찾는 것

두 번째로 saddle point problem은 robust한 분류기가 달성해야하는 정량적인 측정을 제시합니다. 특히 $\theta$가 거의 사라는 risk가 의미하는 것은, 해당 모델이 공격 모델에 의해 지정된 공격에 완벽하게 robust하다는 것을 의미합니다. 

 

본 논문에서는 안장점 문제의 구조를 심층 신경망의 맥락에서 조사합니다. 그리고 조사는 광범위한 adversarial attack에 대해 높은 저항력을 가진 모델을 생성하는 훈련 기술로 이어집니다. 그에 앞서 adversarial example에 대한 이전 연구를 검토하고, 위의 공식에 들어맞는다는 것에 대해 자세히 설명합니다.

2.1 A Unified View on Attacks and Defenses

Adversarial examples에 대한 이전 연구는 2개의 질문에 초점을 맞추었습니다.

• Attack: 어떻게 적은 변형만 가해진 강한 공격을 만드는가?
• Defense: 어떻게 Adversarial example이 없거나 찾기 힘들게 모델을 훈련시킬수 있는가?

공격의 경우, FGSM(Fast Gradient Sign Method)가 있다. Loss 값에 대해 그레디언트를 계산하고, sign 값에 $\epsilon$만큼 이미지를 변경하여 이미지를 변경하는 방식이다. 본 논문에서는 같은 $L_∞$ attack인 PGD(Project Gradient Descent) attack을 이용한다. 이는 매우 강력한 공격 방법 중 하나이며, FGSM을 step 단위로 나눠서 사용하는 방식의 공격이다. 그 외 특징은 random perterbation이 있는 FGSM 방식도 제안되었다. 이러한 모든 접근 방법은 inner maximization, 즉 Loss를 최대로 만드는 adversarial example을 만들기 위한 접근법으로 보일 수 있습니다.

• FGSM $$ x + \epsilon \text{sign}(\nabla_x J(\theta, x, y))$$
• PGD $$ x^{t+1} = \prod_{x+\mathcal{S}}(x^t + \alpha \text{sign} (\nabla_x J(\theta, x, y))) $$

Defense 측면에서는 FGSM으로 생성된 adversarial examples로 증강된 Training set을 사용합니다. 단순화 된 강력한 최적화 문제를 해결하기 위해 training dataset을 모두 FGSM으로 생성된 adversarial examples로 구성하기도 합니다. 

 

 

3. Towards Universally Robust Networks

현재 adversarial examples에 관한 연구는 일반적인 방어 메커니즘 혹은 그런 방어에 대한 공격에 초점을 맞추고 있습니다. 위에서 보았던 min-max 공식화의 중요한 특징은 작은 adversarial loss를 달성하면, 허용된 어떤 공격도 네트워크를 속일 수 없음을 보장한다는 것입니다. Inner maximization은 loss를 가장 높이는 공격방식을 의미하지만, 이러한 예제 자체는 정의에 따라 존재하지 않습니다. 그럼 min-max 공식에서 좋은 값을 갖는 방식에 대해 알아보겠습니다.

 

불행하게도 안장점 문제가 제공하는 전반적인 보장은 분명 유용하지만, 실제로 적절한 시간 내에 좋은 해결책을 찾을 수 있는지는 확실하지 않습니다. 안장점 문제를 해결하는 것은 2개의 문제, non-convex outer minimization problem 과 non-concave inner maximization problem을 해결하는 것을 포함합니다. 

 

본 논문의 중요한 기여 중 하나는 실제로 안장점 문제를 해결할 수 있다는 것을 보여주는 것입니다. 특히 non-concave inner problem에 의해 주어진 구조에 대해 논의합니다. 우리는 이 문제가 놀라울정도로 다루기 쉬운 구조인 local maxima 의 구조를 가지고 있다고 주장합니다. 이 구조는 또한 궁극적인 first-order adversary 를 가리킵니다. Section 4, 5에서 결과적으로 네트워크가 충분히 큰 경우 훈련된 네트워크가 광범위한 공격에 대해 실제로 강력하다는 것을 보여줍니다.

3.1 The Landscape of Adversarial Examples

Inner problem은 adversarial example을 만드는 것과 동일하며 이미 자주 사용하는 FGSM과 같은 공격 방법들이 있습니다. FGSM을 이용해 adversarially train된 모델들이 이미 FGSM 같은 약한 공격에 대해 robust 하다는 것들을 보인 논문들이 있으며 본 논문들은 그러한 사전 연구들을 참조하였습니다.

 

본 논문의 실험에서는 MNIST와 CIFAR-10에 대해 PGD attack을 이용한 PGD adversarial train을 하였고, 랜덤 포인트에서 시작하였습니다. 놀랍게도 다양한 랜덤 포인트에서 출발했지만 만들어진 adversarial example들은 비슷한 loss값을 가졌습니다. 이는 곧 해결하고자 했던 min-max formulation을 PGD를 통해 충족시키는 것이 가능하다는 것입니다. 

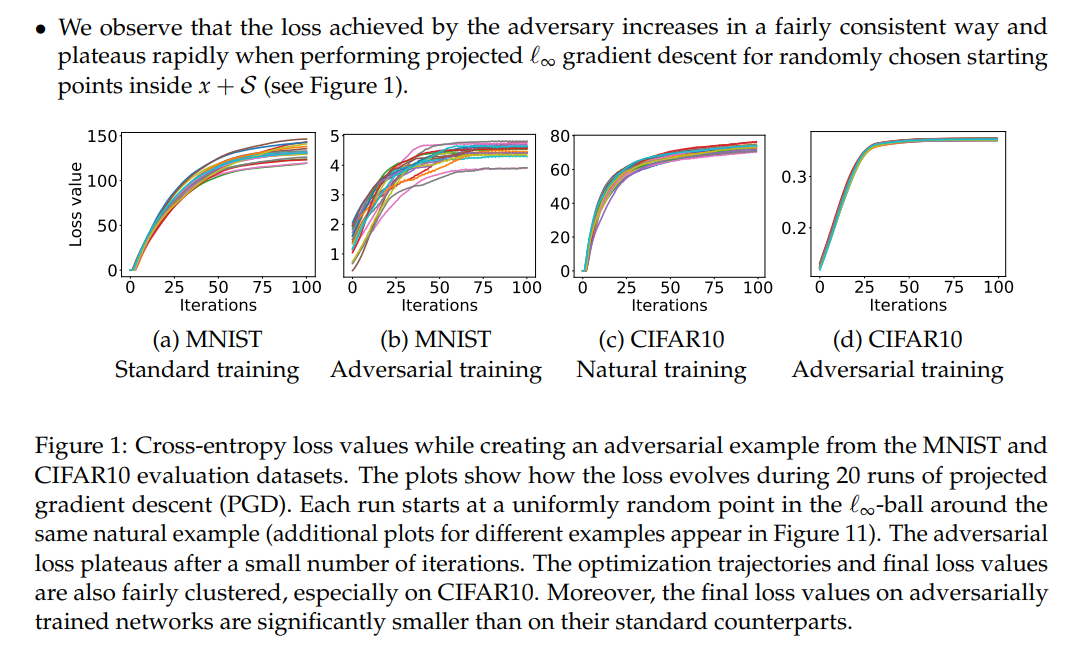
위 실험 결과를 통해 loss 값이 수렴하는 것과, adversarial training이 된 모델의 loss가 standard training의 loss와 비교했을 때 월등히 작다는 것을 확인할 수 있습니다.

 

Figure 2sms 크로스 엔트로피 loss에 의해 주어진 local maxima에 대한 값입니다. 각각의 MNIST, CIFAR-10에 대해 동일하게 랜덤 포인트에서 실행한 결과입니다. 파란색 히스토그램은 standard network, 빨간색 히스토그램은 adversarial trained network에 대한 결과로 PGD보다 더 loss를 낮게 만드는 방법은 찾기 힘들다는 것을 보여줍니다.

 

이 밖에도 논문에서 더 자세히 이에 대한 내용을 설명하고 있으니, 더 자세한 내용은 원본 논문을 참고해주세요. 이런 증거들의 뒷받침으로 PGD는 굉장히 강력한 first-order approach라 할 수 있습니다.

 

3.2 First-Order Adversaries

PGD로 만들어진 예제들은 비슷한 loss 값을 가지며 이는 first-order information에 의존하는 공격, 즉 first-order adversaries 에 대해 robust하다는 것을 뜻합니다. 실제 실험 결과 first-order[입력값에 대한 loss 의 그레디언트만 이용하는 경우] 중 PGD attack보다 더 나은 local maxima를 만드는 공격을 찾을 수 없었고, 이는 곧 PGD에 대해 충분히 robust하다면 다른 first-order 공격들에 대해서도 충분히 robust 할 것이라 말합니다.

 

실제 학습에 있어서도 SGD 같은 first-order method 를 사용하는 것이 일반적이기 때문에 first-order attack 만으로도 충분히 universal한 적용을 할 수 있다고 합니다. 추가적인 black-box attacks에 대해서도 robust하게 동작하며 transfer attack 등에 대해서도 robust 하다는 것을 실험으로 보였습니다. 

 

3.3 Descent Directions for Adversarial Training

PGD Training 을 한 모델이 매우 robustness 하다는 것과 학습이 잘되느냐는 다른 문제입니다. 일반적으로 SGD에 기반한 minimization 기법을 통해 모델을 학습시키는데 이런 방식으로 안장점 문제도 잘 해결할 수 있는가? 라는 의문을 제기할 수 있습니다. 이는 이전의 연구인 Danskin's theorem에 따라 연속적으로 미분가능한 함수에 대해서는 학습이 잘 될 것이다 라는 것을 말하비다. 그러나 보통의 모델은 ReLU나 max-pooling 과 같은 비선형 계층이 있기 때문에 완전히 미분가능하지는 않습니다. 그럼에도 불구하고 SGD를 이용해 학습을 진행했을 때 안장점 문제를 최적화하는 방향으로 잘 학습되었다는 것을 실험을 통해 보였습니다.

 

 

4. Network Capacity and Adversarial Robustness

위 이미지는 standard와 adversarial로 학습한 decision boundary 그림입니다. 오른쪽은 adversarial training을 통해 $\epsilon$값에 딱 맞춰 모델이 non-linear 하게 학습됨을 확인할 수 있습니다.

 

본 논문에서의 실험 결과는 capacity가 robustness에 있어 매우 중요하며, 강력한 adversary에 대해 train 하는 데에도 중요하다는 것을 보여줍니다.

위 결과는 MINST 데이터셋과 CIFAR-10 데이터셋에 대해 간단한 convolution network를 적용하고, 그 크기를 2배씩 키워가며 관찰한 실험 결과입니다. 4개의 필터로 구성된 convolution 레이어와 64개의 unit으로 구성된 FC hidden layer로 구성됩니다. convolution 레이어에는 max-pooling 레이어 2개가 뒤따르고 adversarial examples 들은 $\epsilon=0.3$으로 구성됩니다.

 

CIFAR-10 데이터셋의 경우 ResNet 모델을 사용하였으며 data augmentation을 위해 random crops, flips, 표준화 를 진행하였습니다. capacity를 증가시키기 위해 layer를 10의 배수로 결합시키도록 변환하였습니다.

 

위 실험들을 통해 몇가지의 현상들을 관찰할 수 있었습니다.

1. Capacity의 증가만으로도 adversarial training에 도움이 된다.
2. FGSM adversary만으로는 robustness 를 충분히 증가시킬 수 없다. $\epsilon$값을 증가시킬 경우, label leaking이 발생한다.
3. Capacity가 작으면 adversarial training 자체가 잘 안된다.
4. Capacity를 증가시키면 saddle point problem의 값이 감소한다.
5. Capacity의 증가와 강력한 adversary는 transferability를 감소시킨다.

 

5. Experiments: Adversarially Robust Deep Learning Models

결론적으로 robustness한 모델을 만들기 위해서 2가지를 집중해야합니다.

1. 네트워크는 충분히 높은 capacity를 가져야 한다.
2. 강력한 adversary를 사용해야 한다.

위 Figure 4에 대한 결과를 분석해보면 MNSIT에서는 capacity가 증가함에 따라 정확도가 증가하고, CIFAR-10에서는 FGSM으로 학습된 모델에 대해서는 label leaking이 발생하며 PGD attack에 대해서는 방어를 할 수 없다는 것을 확인할 수 있습니다. 부가적으로 더 wide한 모델에서 정확도가 더 높게 나온다는 것도 확인할 수 있습니다. 

학습 과정동안의 크로스 엔트로피 그래프입니다. CIFAR-10에서 2번의 급격한 감소는 training step 크기의 감소로 생긴 결과입니다. 

그 외에도 $\epsilon$값을 변경하며 실험해보고, $L_2$ attack에 대한 실험도 진행합니다. $\epsilon$의 경우 그 값이 조금만 증가해도 정확도가 많이 떨어지며, $L_∞$ attack에 대해 robust하다면 $L_2$ attack에 대해서도 어느 정도 robust함을 확인할 수 있었습니다.

 

Table 1은 MNIST 데이터셋에 대한 attack 실험 결과를 정리한 표입니다. adversarial training 을 했을 때 강력한 PGD attack에 대해서도 89.3%로 잘 방어해내고 있다는 것을 확인할 수 있습니다. 아키텍처는 같고 새롭게 학습한 모델에서 transferability attack을 한 경우(A')에 대해서도 방어를 잘 하고 있음을 확인할 수 있습니다.

• $A$: white-box attack
• $A'$: 모델의 구조는 같고 weight가 다른 attack
• $B$: 모델의 구조도 다른 black-box attack

 

Table 2는 CIFAR-10 에 대한 실험결과를 정리합니다. Natural 의 87.3% 와 PGD의 45.8% 라는 수치를 비교해보면 일반 benign example에 대해서도 잘 분류를 하고, PGD attack에 대해서도 45.8%로 어느 정도의 robustness를 보여주고 있습니다. 

• $A$: white-box attack
• $A'$: 모델의 구조는 같고 weight가 다른 attack
• $A_{nat}$: natural example로만 학습된 모델에 대한 공격

 

6. Conclusion

본 논문의 발견은 심층 신경망이 adversarial attack에 저항력을 가질 수 있다는 증거를 제공합니다. 이론과 실험에서 확인할 수 있듯이 신뢰할 수 있는 adversarial training 방법을 설계할 수 있습니다. FGSM 같은 one-step adversaries 가 아닌 PGD 같은 multi-step method를 이용하면 강력한 공격에 대해 충분히 robust 하다는 것을 보였습니다. min-max formulation 중 안쪽의 inner maximization problem 을 해결하는 것을 local maxima 를 잘 찾는 PGD attack으로 충분하다는 것을 보였습니다.

 

MNIST 같은 쉬운 데이터셋의 경우에는 매우 높은 robust accuracy를 달성하였습니다. CIFAR-10에 대해서는 아직 그정도로 우수한 성능까지는 도달하지 못했습니다. 하지만 결과를 통해 본 논문에서 제시한 기술들이 네트워크의 robustness 를 크게 증가시킨다는 것을 보여줍니다. 앞으로 이 방향에 대한 후속 연구를 통해 데이터셋에 대해 더 robust 한 네트워크를 만드는 것으로 이어질 것이라 믿습니다.

 

 

 

Reference : https://arxiv.org/abs/1706.06083

Towards Deep Learning Models Resistant to Adversarial Attacks