구현이라기보단 제가 스스로 이해하기 위해 주석 및 설명을 달아놓는 포스팅입니다. 개념 설명이 아닌 포스팅이라 코드를 보실 분 아니면 넘어가셔도 좋을 것 같습니다.
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 계층 생성
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1 : t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x : 입력 데이터, t : 정답 레이블
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads

# 계층 생성
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()self.layers는 OrderedDict 로 아래와 같은 형태로 저장되어 있습니다. Affine - Relu - Affine 인스턴스를 초기화하여 { Affine1 : Affine 클래스의 인스턴스, Relu1 : Relu 클래스의 인스턴스, Affine2 : Affine 클래스의 인스턴스 }
또한 소프트맥스와 로스는 lastLayer라는 인스턴스 변수에 따로 초기화하여 저장합니다.
Dict 자료형은 순서를 구분하지 않는데 순전파와 역전파에서는 순서가 중요하기 때문에 OrderedDict 를 사용합니다. 이 때 자세한 생성자를 확인하려면 import 로 가져온 common 폴더의 layers 파일이 필요합니다. layers 파일에는 Relu, Sigmoid, Affine 을 당연히 포함하구 추후 CNN 에서 사용할 컨볼루션, 풀링, 배치 정규화, Dropout 등등의 코드가 구현되어 있습니다. layers 코드를 보고 싶으면 더보기 를 눌러주시면 확인 가능합니다.
import numpy as np
from common.functions import *
from common.util import im2col, col2im
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
# 가중치와 편향 매개변수의 미분
self.dW = None
self.db = None
def forward(self, x):
# 텐서 대응
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 입력 데이터 모양 변경(텐서 대응)
return dx
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 손실함수
self.y = None # softmax의 출력
self.t = None # 정답 레이블(원-핫 인코딩 형태)
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size: # 정답 레이블이 원-핫 인코딩 형태일 때
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dx
class Dropout:
"""
http://arxiv.org/abs/1207.0580
"""
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
class BatchNormalization:
"""
http://arxiv.org/abs/1502.03167
"""
def __init__(self, gamma, beta, momentum=0.9, running_mean=None, running_var=None):
self.gamma = gamma
self.beta = beta
self.momentum = momentum
self.input_shape = None # 합성곱 계층은 4차원, 완전연결 계층은 2차원
# 시험할 때 사용할 평균과 분산
self.running_mean = running_mean
self.running_var = running_var
# backward 시에 사용할 중간 데이터
self.batch_size = None
self.xc = None
self.std = None
self.dgamma = None
self.dbeta = None
def forward(self, x, train_flg=True):
self.input_shape = x.shape
if x.ndim != 2:
N, C, H, W = x.shape
x = x.reshape(N, -1)
out = self.__forward(x, train_flg)
return out.reshape(*self.input_shape)
def __forward(self, x, train_flg):
if self.running_mean is None:
N, D = x.shape
self.running_mean = np.zeros(D)
self.running_var = np.zeros(D)
if train_flg:
mu = x.mean(axis=0)
xc = x - mu
var = np.mean(xc**2, axis=0)
std = np.sqrt(var + 10e-7)
xn = xc / std
self.batch_size = x.shape[0]
self.xc = xc
self.xn = xn
self.std = std
self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * mu
self.running_var = self.momentum * self.running_var + (1-self.momentum) * var
else:
xc = x - self.running_mean
xn = xc / ((np.sqrt(self.running_var + 10e-7)))
out = self.gamma * xn + self.beta
return out
def backward(self, dout):
if dout.ndim != 2:
N, C, H, W = dout.shape
dout = dout.reshape(N, -1)
dx = self.__backward(dout)
dx = dx.reshape(*self.input_shape)
return dx
def __backward(self, dout):
dbeta = dout.sum(axis=0)
dgamma = np.sum(self.xn * dout, axis=0)
dxn = self.gamma * dout
dxc = dxn / self.std
dstd = -np.sum((dxn * self.xc) / (self.std * self.std), axis=0)
dvar = 0.5 * dstd / self.std
dxc += (2.0 / self.batch_size) * self.xc * dvar
dmu = np.sum(dxc, axis=0)
dx = dxc - dmu / self.batch_size
self.dgamma = dgamma
self.dbeta = dbeta
return dx
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 중간 데이터(backward 시 사용)
self.x = None
self.col = None
self.col_W = None
# 가중치와 편향 매개변수의 기울기
self.dW = None
self.db = None
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0,2,3,1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h*self.pool_w)
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return xlayers 에 저장된 각 키의 value 들에 대해 순전파를 진행합니다. layer는 위에서 선언한대로 Affine, Relu, Affine 이 됩니다. 소프트맥스와 로스 계층은 layers 에 포함되어 있지 않고, lastLayer에 따로 저장되어 있기 때문에 SoftmaxWithLoss 계층은 실행되지 않습니다.
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1 : t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracyloss 는 pridict 를 거쳐 나온 값(Score 값에 대해) 마지막 레이어, 즉 SoftmaxwithLoss 레이어의 forward 를 진행한다는 것인데 이는 곧 예측값과 정답값 과의 크로스 엔트로피를 구한다는 것과 동일합니다.
또한 여기서 알아야 하는 개념이, 학습 중일때는 확률분포 사이의 거리를 재기 위해 softmax층과 loss층이 필요합니다. 그러나 학습이 끝나고 추론을 할 때는 softmax층과 loss층의 계산은 필요하지 않습니다. 오직 최대의 점수가 나오는 항만 알면 됩니다. 왜냐면 softmax 자체가 일종의 정규화이고, loss 층은 정답 라벨과 차이를 구하는 건데 추론 과정은 이 연산이 필요없기 때문입니다.
accuracy 는 정답률을 나타내는데, 이 때 score 까지만 알면 되기 때문에 predict 까지만을 수행해줍니다.
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads역전파를 계산하는 부분으로, 마지막 부분에 각 계층의 그레디언트 계산값을 dict 형으로 반환합니다.
lastLayer에 대해서 들어오는 Upper gradient가 없으므로 초기값을 1로 설정하고, 마지막 계층 SoftmaxWithLoss 부터 시작하여 거꾸로(layers.reverse()) 계산을 수행합니다.
그 이후 ordereddict 형태로 저장되어 있는 self.layers 에 ['키'] 값을 넣으면 value 값이 나오게 됩니다. 이 때의 value 는 각각 Affine 클래스의 인스턴스들이 될 겁니다. Affine 클래스의 dw와 db 값을 grads dict 에 저장하고 grads 를 반환합니다.
MNIST 데이터셋을 학습을 하는 코드입니다. 이 전 포스팅에도 비슷한 설명을 했으니 간단하게 넘어가도록 하겠습니다.
TwoLayerNet을 불러와 입력은 784개 노드, 은닉층은 50개 노드, 출력층은 10개를 가지는 인스턴스를 network로 생성합니다. 그 이후 하이퍼 파라미터들을 지정해줍니다. x_train 은 6만장의 MNIST 데이터를 가지고 있는데, 이 때 flatten 해서 저장하기 때문에 60000 * 784 행렬이 됩니다. 따라서 shape[0]이 곧 60000, 훈련 데이터의 크기가 됩니다.
# coding: utf-8
import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
import pickle
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
#grad = network.numerical_gradient(x_batch, t_batch) # 수치 미분 방식
grad = network.gradient(x_batch, t_batch) # 오차역전파법 방식(훨씬 빠르다)
# 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print(train_acc, test_acc)
with open("neuralnet.pkl", 'wb') as f:
pickle.dump(network.params, f)반복문부터 살펴보면 iters_num 횟수만큼 반복을 진행합니다. 60000만 장 중 설정한 배치 사이즈인 100장을 랜덤하게 선택하는 코드입니다. 우선 np.random.choice(60000, 100) 을 수행하면 0~59999 중 랜덤하게 중복을 허용하여 100개를 선택하여 저장합니다. 그 이후 각각 train 데이터에서 batch_mask에 해당하는 인덱스의 데이터들을 뽑아서 batch 에 저장합니다.
이 때 이 코드는 살짝 문제가 있는 코드인데, 각 반복마다 계속해서 동일한 값을 뽑을 수 있기 때문에 epoch 를 정의하는 것에 논리적으로 오류가 있습니다. 이를 해결하기 위해서는 train 데이터를 섞고(shuffle) 일정한 크기로 나누어 차례대로 수행하는 방법이 있는데 이는 추후 코드에서 소개하도록 하겠습니다.
network 인스턴스의 gradient 를 통해 가중치들이 저장된 dict 을 반환받습니다. 그 이후 반복문을 통해 grads의 key로 반복을 수행하며 학습률 * grad[key] 값을 빼주면서 networks 의 params[key] 를 갱신하는 것이죠.
그 이후 loss 메서드를 통해 x_batch 와 t_batch 와의 loss 를 구해주고, 그를 train_loss_list 에 추가합니다.
if 문은 성능을 측정하는 코드이고 매 번 측정하는 것이 아닌 i % iter_per_epoch == 0: 일때, 즉 600번 학습이 진행되었을 때마다 성능을 측정하고 출력하는 코드입니다.
마지막의 with 문은 pickle 라이브러리를 사용하여 학습이 끝난 모델을 저장하기 위한 코드입니다. 저장할 때는 load 를 사용하고 불러올 때는 open 을 통해 학습 모델을 저장하고 불러올 수 있습니다.
# 불러오기 코드
with open("파일명", 'rb') as f:
network = pickle.load(f)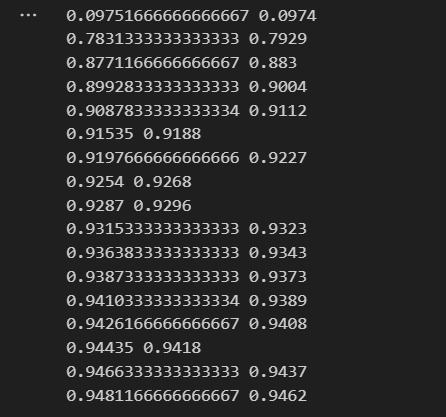
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
x_batch = x_train[:3]
t_batch = t_train[:3]
grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)
# 각 가중치의 절대 오차의 평균을 구한다.
for key in grad_numerical.keys():
diff = np.average( np.abs(grad_backprop[key] - grad_numerical[key]) )
print(key + ":" + str(diff))수치 미분으로 구한 gradient 와 역전파로 구한 gradient 의 차이를 체크해보는 코드입니다. 같은 데이터에 대해 두 행렬에 대해 각각 원소의 차에 절댓값을 씌우고 평균을 구해서 출력하는 코드입니다.
W1:1.7923133704172904e-10
b1:8.316892715975544e-10
W2:7.34206712831309e-08
b2:1.4689727577260613e-07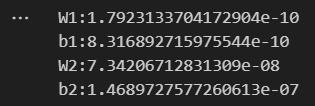
실행해보면 아주 작은 오차가 발생하는 것을 확인할 수 있습니다.
Reference :
밑바닥부터 시작하는 딥러닝 - 사이토 고키
https://github.com/WegraLee/deep-learning-from-scratch
'딥러닝(DL) > 딥러닝 기초' 카테고리의 다른 글
| Generative model vs Discriminative model (생성 모델과 판별 모델) (1) | 2024.01.15 |
|---|---|
| [DL] 선형 회귀 ( Linear Regression ) (0) | 2023.09.02 |
| [DL] 역전파 ( Backward-propagation ) (0) | 2023.08.21 |
| [DL] 학습 알고리즘 구현 ( 2층 신경망 ) (0) | 2023.08.18 |
| [DL] 경사 하강법 ( Gradient Descent ) (0) | 2023.08.17 |