LoRA: Low-Rank Adaptation of Large Language Models (ICLR 2022)

 

 

 

 

LoRA(Low-Rank Adaptation) 은 PEFT(Parameter Efficient Fine Tuning) 기법 중 대표적인 예시로, pretrained model의 모든 weight를 fine-tuning 하는 방법 대신 pretrained model weight를 모두 freeze하고, downstream task를 수행하기 위해 학습이 가능한 rank decomposition matrice를 추가함으로써 효율적으로 fine-tuning하는 방법을 제안하는 논문입니다.

 

기존의 PEFT를 위해 제안되었던 방법들은 adapters를 사용하는 것이었습니다. 여기서 말하는 adapters란 이미 학습이 완료된 모델, pre-trained model의 사이사이에 학습 가능한 작은 feed-forward networks를 삽입하는 구조를 뜻합니다.

 

이러한 adapter 기반 방법론 외에도 다양한 PEFT 방법론들이 제안되었는데, 기본적으로 adapter와 중간중간에 학습 가능한 파라미터를 삽입했다는 아이디어가 비슷하지만, rank decomposition 행렬을 삽입함으로써 구조적으로 조금 다른 PEFT 방법입니다. 2021년에 나온 논문이지만 최근에도 LoRA의 다양한 변형이 나오고 있는 만큼 대표적인 PEFT 방법 중 하나입니다.

---

LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS

 

1 INTRODUCTION

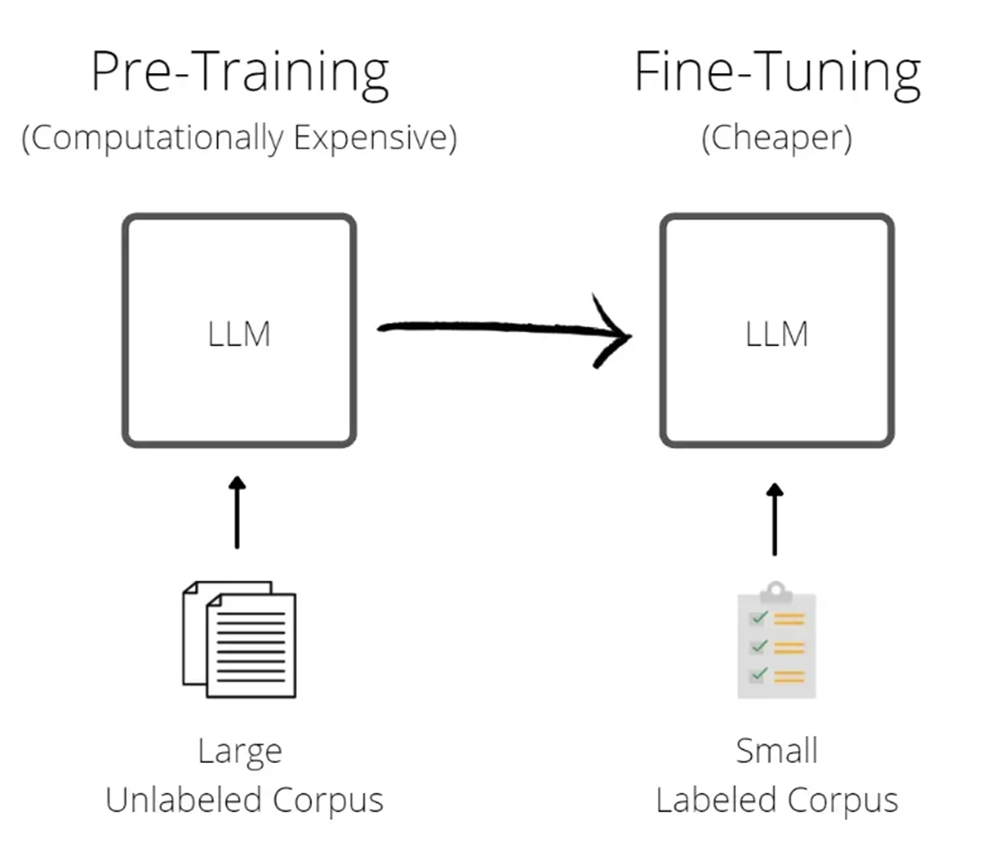
NLP 분야의 많은 응용은 pre-trained LLM을 여러 downstream task로 적용하는 방법을 사용합니다. 이런 적용(adaptation)은 일반적으로 pre-trained model의 모든 메개변수를 업데이트 하는 Fine-tuning을 통해 수행됩니다. Pre-trained된 model을 그대로 task에 적용시키는 것보다, task에 맞게 fine-tuning하여 사용하는 것이 성능이 훨씬 좋다는 것이 다양한 task 들에 대해 입증되었습니다.

 

Pretrained language model은 모델의 모든 파라미터를 업데이트 하는 fine-tuning 방법을 통해 다양한 downstream task에 적용되어 왔습니다. 하지만, 정작 업데이트에 사용되는 파라미터는 극히 일부이기 때문에 비효율적으로 자원을 사용하게 됩니다. 따라서 이전부터 downstream task를 위해 external module을 학습하거나, 몇몇 파라미터만 adapt하는 방식이 제안되어 왔으며, 각각의 task를 수행하기 위해 pre-trained model에 적은 양의 task-specific parameter를 저장하고 불러오는 방법이 제안되어 왔습니다. 이런 방법들은 배포 할 경우 운영에 대한 효율성이 크게 향상되었습니다.

 

그러나 기존의 방식들은 종종 model의 depth를 늘림으로써 inference latency(추론 지연 시간)가 유도되거나, 모델의 입력 가능한 문장 길이를 줄여야 하기 때문에 효율성과 model의 퀄리티 간의 trade off를 고려해야 했습니다. 

 

 

따라서 본 논문에서는, over-parametrized model이 실제 낮은 고유 차원에 있음을 보여주는 선행 연구들을 통해 영감을 받아, 모델을 adaptation 할 때의 가중치의 변화 또한 low intrinsic rank를 가지고 있다고 가정하고 LoRA를 제안합니다.

 

LoRA를 사용하면 사전 학습된 가중치를 고정된 상태로 유지하면서 대신 adaptation 중 레이어의 변화에 대한 rank decomposition matrix들을 최적화하여 신경망의 일부 레이어를 간접적으로 학습할 수 있습니다. GPT-3 175B를 예를 들어보면 전체 rank가 12,288만큼 높은 경우에 대해서도 매우 낮은 rank인 1이나 2로 충분하다는 것을 보임으로써 LoRA가 스토리지 및 컴퓨팅 효율성을 모두 높일 수 있음을 보여줍니다.

 

Terminologies and Conventions

본 논문은 Transformer 아키텍처를 참조하며, 크기에 대해 기존 용어를 그대로 사용합니다.

• $d_{model}$ : Transformer 레이어의 입력 및 출력 차원의 크기
• $W_q, W_k, W_v, W_o$ : Self-attention 모듈 내 query, key, value, output projection 행렬
• $W$ 또는 $W_0$ : 사전 학습된 가중치 행렬
• $\Delta W$ : Adapatation 중 누적된 gradient 업데이트
• $r$ : LoRA 모듈의 rank

 

2 PROBLEM STATEMENT

$\Phi$로 parameterize된 사전 학습된 autoregressive model $P_{\Phi}(y|x)$가 주어졌다고 가정합니다. 예를 들어 $P_{\Phi}(y|x)$는 Transformer 아키텍처를 기반으로 하는 GPT와 같은 일반적인 multi-task learner 일 수 있습니다. 여러 downstream 조건부 텍스트 생성 task에 이 사전학습된 모델을 적용하는 상황을 고려합니다. 각 다운스트림 task 는 context-target 쌍의 학습 데이터셋으로 표기됩니다.

 

$$ \mathcal{Z}=\{(x_i, y_i)\}_{i=1, ..., N} $$

 

여기서 $x_i$와 $y_i$는 모두 토큰 시퀸스입니다. 요약의 경우 $x_i$는 기사의 내용이 되고, $y_i$는 기사의 요약이 됩니다.

전체 fine-tuning 중 모델은 사전 학습된 가중치 $\Phi_0$로 초기화되고, 조건부 언어 모델링 목적 함수를 최대화하기 위해 반복적으로 기울기를 따라 $\Phi_0+\Delta \Phi$로 업데이트 됩니다.

 

$$ \underset{Θ}{\text{max}} \sum_{(x,y)\in \mathcal{Z}} \sum_{t=1}^{|y|} \log (P_{\Phi}(y_t|x, y_{<t}))$$

 

본 논문은 low-rank 표현을 사용해 계산 및 메모리에 대해 효율적인 $\Delta \Phi$를 인코딩 할 것을 제안합니다. 즉 전체 가중치가 아닌 훨씬 작은 크기의 파라미터 집합으로 인코딩된 $\Delta \Phi = \Delta \Phi(Θ)$에서 $Θ$에 대한 최적화를 수행합니다.

 

$$ \underset{Θ}{\text{max}} \sum_{(x,y)\in \mathcal{Z}} \sum_{t=1}^{|y|} \log (p_{\Phi_0 + \Delta \Phi( Θ )}(y_t|x, y_{<t}))$$

 

 

사전 학습된 모델이 GPT-3 175B 인 경우 학습 가능한 파라미터의 수 $|Θ|$는 $|\Phi|$의 $0.01\%$ 정도로 경량화할 수 있습니다.

 

 

3 AREN’T EXISTING SOLUTIONS GOOD ENOUGH?

본 논문이 해결하려는 문제는 결코 새로운 문제가 아닙니다. Transfer learning이 시작된 이래 많은 수의 연구들이 모델 adaptation을 보다 파라미터 및 계산 효율적으로 만들기 위해 노력했습니다. 예를 들어 언어 모델링을 사용할 경우 효율적인 adaptation과 관련해 두 가지 주요 전략이 있습니다.

• Adapter layer 추가
• 입력 레이어 activation의 일부 형식 최적화 (Prefix 튜닝)

Adapter layer를 추가하는 것은 Multihead attention의 결과값을 받아 Adapter에 삽입하는 sequential 한 방법입니다. 따라서 이런 방법은 모델의 깊이를 증가시키고, Inference latency(추론 지연 시간)이 발생할 수 있습니다.

 

Prefix-tuning은 최적화하기 어렵고, 이 성능 자체가 trainable parameter non-monotonically하게 변합니다. 또한 Adaptation을 위해 sequence length의 일부를 미리 떼어놔야 하기 때문에 downstream tak를 처리하는데 사용할 수 있는 sequence length가 줄어든다는 문제가 있습니다.

 

 

 

4 OUR METHOD

LOW-RANK-PARAMETRIZED UPDATE MATRICES

• 모든 Dense layer에 적용 가능 (Language 뿐만 아니라 Vision 등에도 적용 가능)
• Down projection과 Up projection 으로 구성
• 가정 : 가중치에 대한 update도 adaptation 중 intrinsic rank가 낮다고 가정 (기존의 over-parameter model의 intrinsic rank가 낮다고 주장하는 paper 기반 가정)
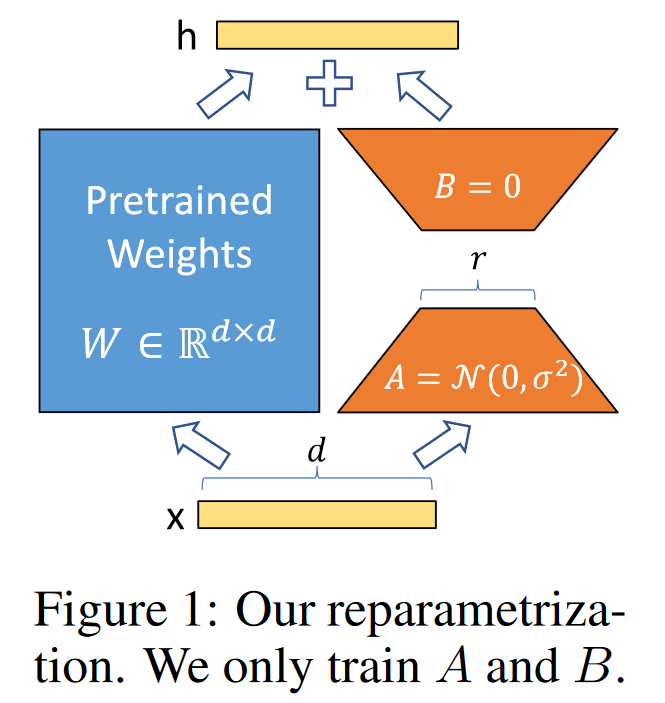
  • Pre-trained weight matrix $W_0$에 대해 이 행렬에 대한 업데이트를 low-rank decomposition을 통해 아래와 같이 표현
  • Gradient 의 변화랑 $\Delta W$를 BA로 approximate 하겠다는 것
  • $W_0$는 frozen (gradient update X)
  • $r$ 차원으로 줄였다가, 원래의 output feature의 차원인 $d$로 늘리고, merge 한다.

 

$$ h = W_0x + \Delta Wx = W_0x + BAx$$

$$ \text{where } B \in \mathbb{R}^{d\times r}\quad , \quad A \in \mathbb{R}^{r\times k} \quad , \quad r ≪ \text{min}(d,k) $$

 

위 방법을 통해 Additional inference latency가 발생하지 않도록 합니다. Downstream task의 weight인 A, B 값을 더해줌으로서 merged weight가 fine-tuning된 weight가 되는 원리로, Inference 시에는 그냥 이 Layer를 통과시켜 주면 됩니다. 만약 original weight 값으로 되돌리고 싶으면 위에서 merge한 weight를 빼면 다시 돌아오게 됩니다.

 

좀 더 디테일한 내용으로는, $A$에는 랜덤 가우시안 초기화를 사용하고 $B$에는 0을 사용하므로 학습 시작 시 $BA=0$입니다.

 

Practical Benefits and Limitations

가장 중요한 이점은 메모리와 스토리지 사용량 감소입니다. Adam으로 학습된 대형 Transformer의 경우 고정 파라미터에 대한 optimizer 상태를 저장할 필요가 없으므로 $r≪d_{model}$ 인 경우 VRAM 사용량을 최대 $2 / 3$ 까지 줄입니다. GPT-3 175B의 경우 학습 중 VRAM 소비를 1.2TB에서 350GB로 줄입니다. $r=4$이고 query와 key projection 행렬만 튜닝되면 체크포인트 크기가 약 1만배 감소합니다. 이를 통해 훨씬 적은 수의 GPU로 학습하고, 입출력 병목 현상을 피할 수 있습니다.

 

또 다른 이점은 모든 파라미터가 아닌 LoRA 가중치만 교환함으로써 훨씬 저렴한 비용으로 배포 중 task 사이를 전환할 수 있다는 점입니다. 이를 통해 사전 학습된 가중치를 VRAM에 저장하는 시스템에서 즉석에서 교환할 수 있는 많은 맞춤형 모델을 생성할 수 있습니다. 

 

그러나 LoRA에도 한계점은 있는데요, 예를 들어 추가 inference 대기 시간을 제거하기 위해 $A$와 $B$를 $W$로 흡수하기로 선택한 단일 forward pass에서 $A$와 $B$가 다른 여러 task에 대한 입력을 일괄 처리하는 것은 간단하지 않습니다. 

 

 

5 EMPIRICAL EXPERIMENTS

BASELINES

• $FT$ : Fine-Tuning
• $FT^{Top2}$ : 마지막 2 레이어만 튜닝
• $BifFit$
• $Adap^H$ : 오리지널 adapter tuning
• $Adap^L$ : MLP 모듈 뒤 LayerNorm 뒤에만 adapter layer 적용
• $Adap^P$ : AdapterFusion
• $Adap^D$ : AdapterDrop

 

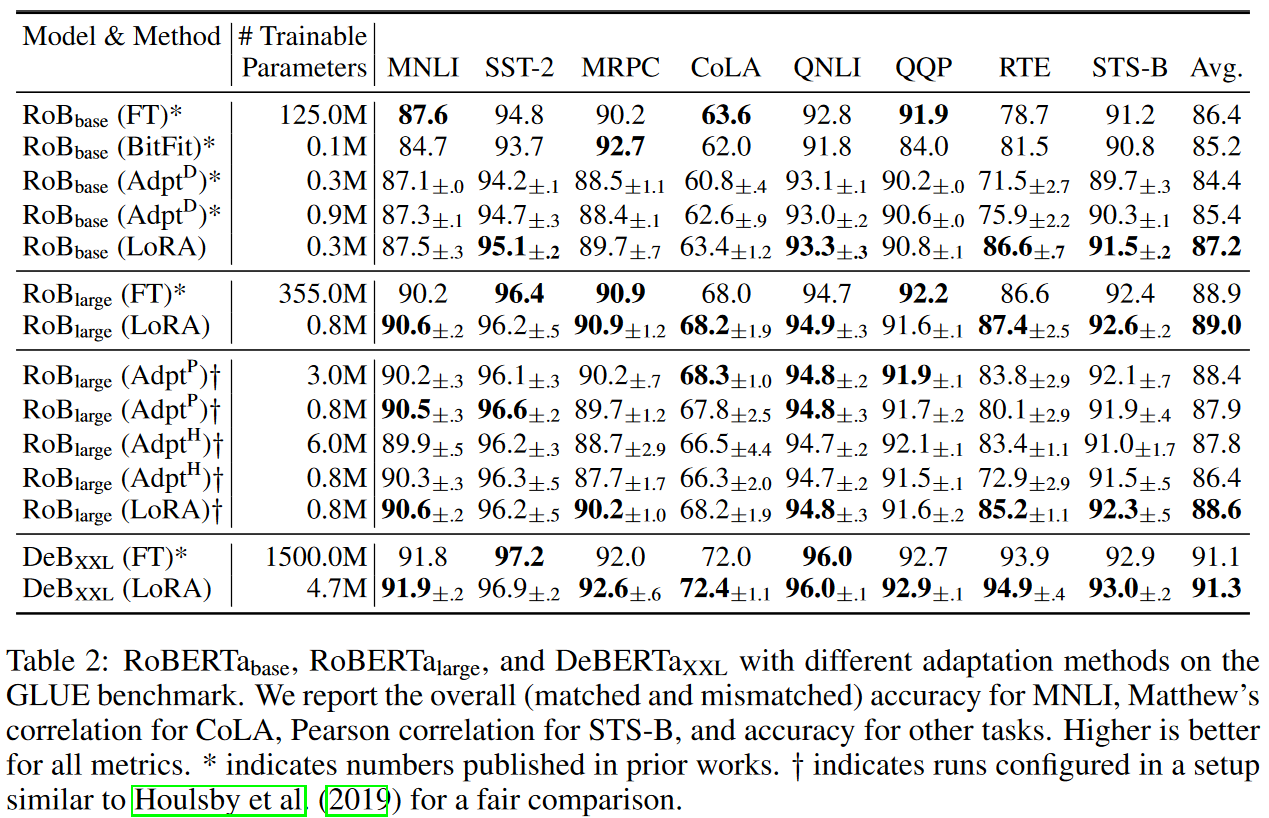
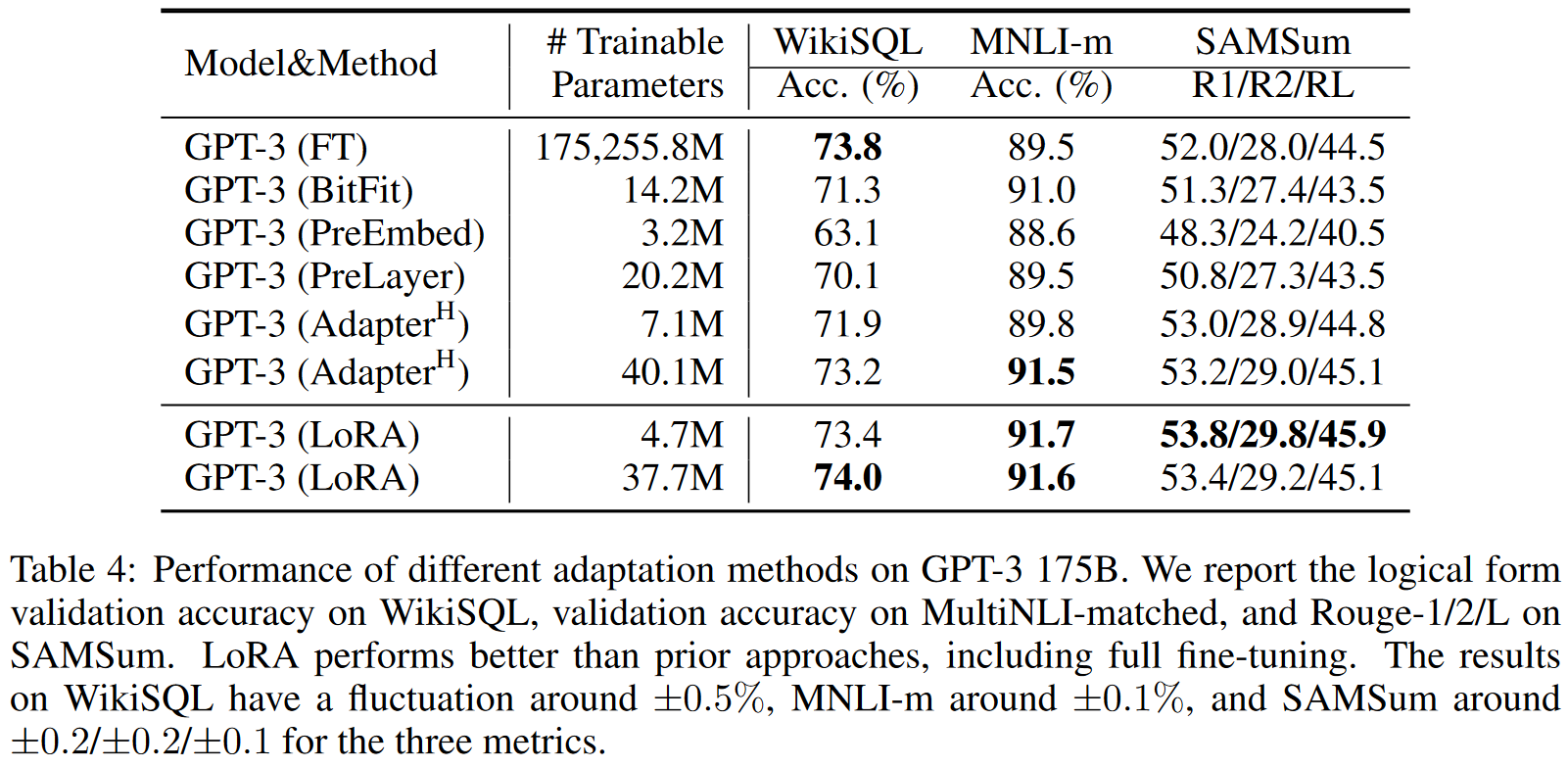
Full Fine-tuning과 유사하고, 기존의 peft 방법보다 향상된 성능을 보이고 있습니다. 또한 아래의 표에서 GPT의 경우

• Parameters : 기존의 0.01% 사용
• VRAM 1.2TB → 350GB
• 체크포인트 크기 : 350GB → 35MB

 

 

Ablation study

1. 어떤 가중치 행렬에 적용해야 효과적인가?

 

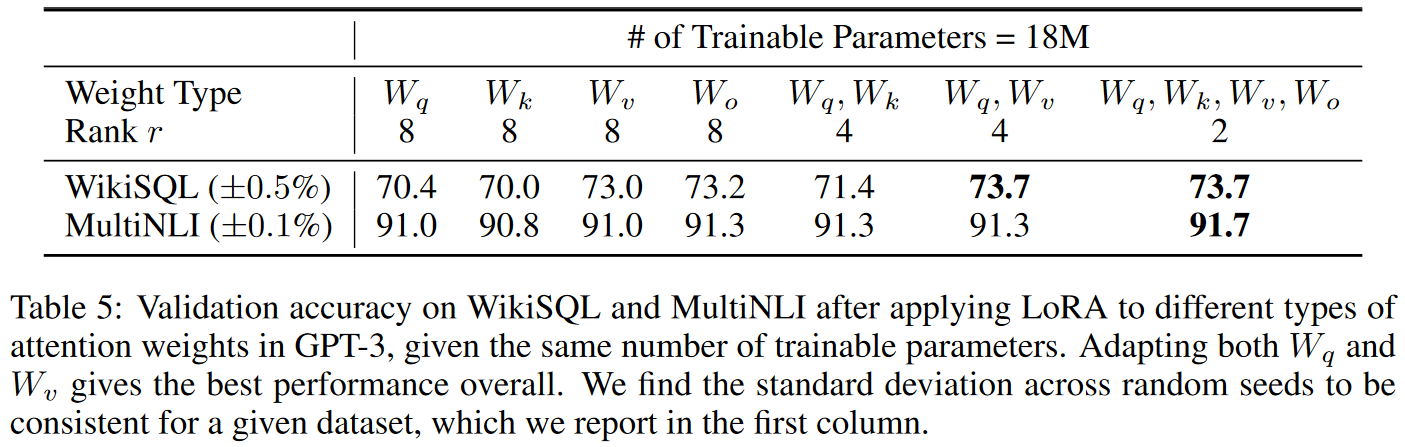
Attention module에 대해 query, key, value, output projection 가중치를 조합해보며 실험한 결과, 각 Task나 model마다 다르다는 결과를 얻습니다. 그러나 일반적으로 단일 Layer에 큰 rank를 사용하는 것보다 여러 Layer에 낮은 rank를 사용하는 것이 효과적이었다고 합니다.

해당 논문에서는 Attention module에 대해서만 실험을 진행했지만, LoRA 모듈은 Embedding이나 Conv layer 같은 다른 Linear layer에도 사용이 가능합니다.

 

2. 가장 효과적인(적절한) rank 는?

 

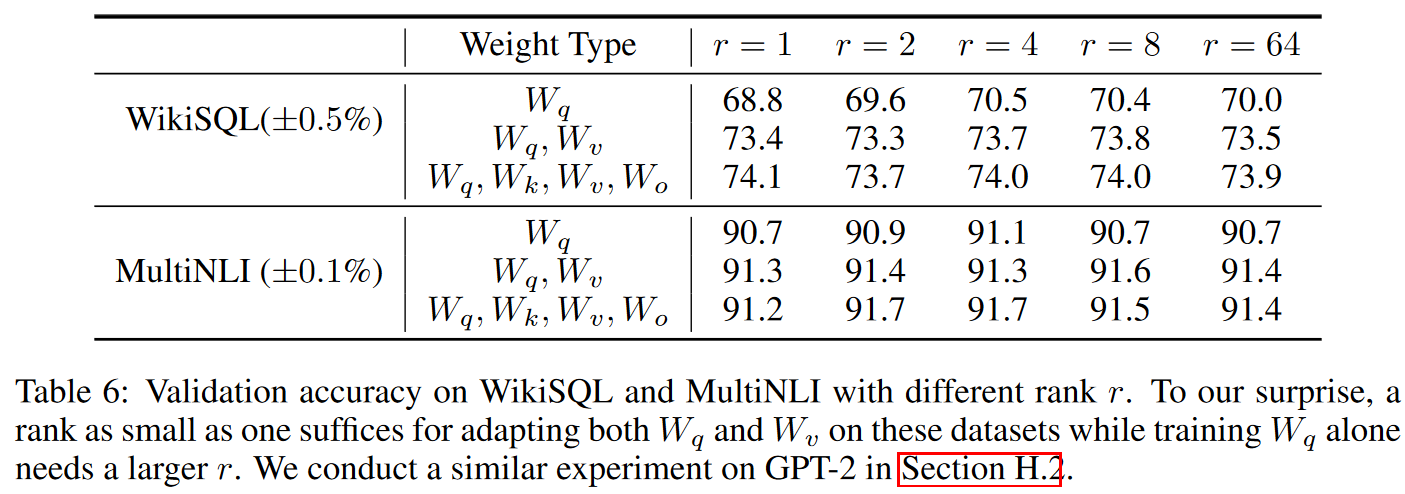
Rank와 성능이 비례하지 않는 결과를 얻었으며, 매우 작은 $r$에 대해서도 뛰어난 성능을 보였습니다. 따라서 본 논문에서는 "update matrix $\Delta W$ could have a small intrinsic rank." 라며 업데이트 가중치 행렬이 작은 intrinsic rank를 가질 것이라고 제안합니다.

 

 

Reference:

LoRA: Low-Rank Adaptation of Large Language Models