뉴럴 네트워크는 데이터를 통해 학습을 할 때 "미분"을 이용하여 학습을 합니다.
$$ f'(x) = \lim_{h \to 0} \dfrac{f(x+h)-f(x)}{h} $$
미분 계수는 극한으로 정의됩니다. 어떤 함수의 순간 변화율을 구하는 것을 의미하고 고등학교 수학 시간에 이미 여러 번 배운 수식이죠. 그런데 딥러닝에서는 컴퓨터한테 극한값이라는 고차원 적인 개념을 알려주고 프로그래밍하기 복잡하기 때문에 엄밀한 미분 계수는 아니지만, 그와 비슷한 값이 나오는 평균 변화율을 사용하게 됩니다.
아이디어는 매우 작은 $h$를 잡게 되면 실제 미분계수와 거의 동일한 값을 가진다는 것이죠. 즉 미분 계수를 다음과 같이 충분히 작은 $h$를 잡아 근사시킵니다.
$$ \dfrac{f(x+h)-f(x)+}{h} $$
이 식처럼 엄밀하게 미분계수의 정의와는 다르지만, 이처럼 아주 작은 차분, 매우 작은 $h$를 잡아 근사시킨 이 함수를 수치 미분(Numerical differentiation) 이라고 부릅니다. 수치 미분을 파이썬으로 구현할 때 가능한 작은 값을 넣으면 미분계수와 더 동일해지기 때문에 아주 작은 값을 넣는다고 생각하는게 일반적이지만 실제로 너무 작은 값을 $h$에 대입하게 되면 반올림 오차(rounding error) 가 발생하게 됩니다.
import numpy as np
print(np.float16(1e-4))
print(np.float16(1e-50))
# 출력 결과:
# 0.0001
# 0.0너무 작은 값을 이용하면 컴퓨터는 반올림을 통해 0으로 계산하게 됩니다. 분모에 $0$이 들어가게 되면 값이 정의되지 않기 때문에 대략 $10^{-4}$ 정도의 값을 사용하는 것이 좋습니다.
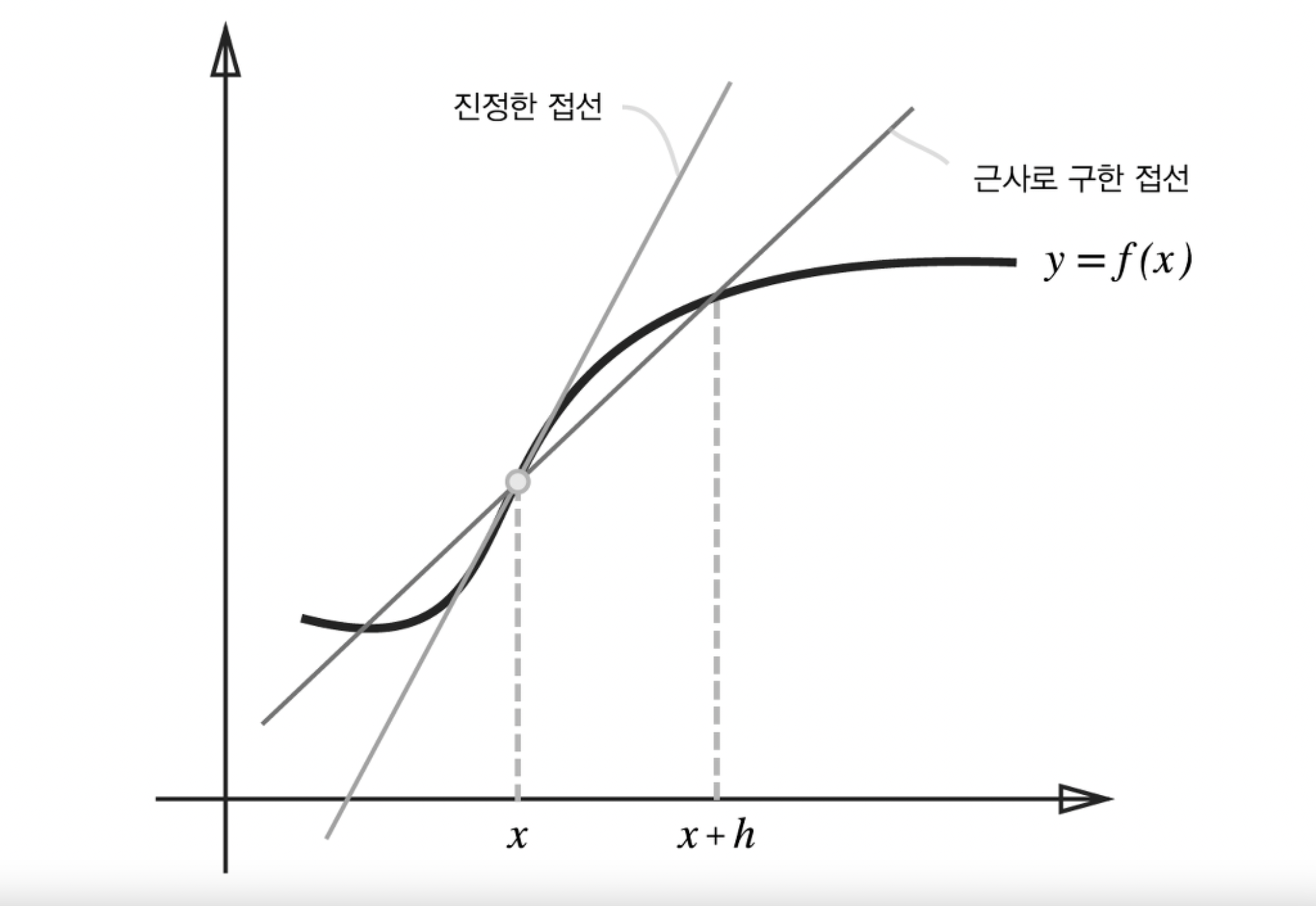
또한 수치 미분으로 구하게 된 함수 $f$의 차분, 즉 $f(x+h)-f(x)$ 의 값은 실제 미분 계수와 오차가 발생하게 됩니다. 미분 계수는 접선의 기울기를 나타내게 되지만 $h$값을 무한히 0으로 좁힐수가 없기 때문에 수치미분값은 근사접선이 나타나게 되는 것이죠.
$$ \lim_{}h \to 0} \dfrac{f(x+h)-f(x)}{h} = \lim_{}h \to 0} \dfrac{f(x+h)-f(x-h)}{2h} $$
위 등식이 성립하므로 수치미분 또한 아래처럼 근사시킬 수 있고, 이렇게 근사시킨 수치미분이 오차가 더 적게 나타납니다.
$$ \dfrac{f(x+h)-f(x-h)}{2h} $$
위처럼 $x+h$와 $x-h$일 때의 함수 $f$의 차분을 계산하는 방법을 중심 차분, 혹은 중앙 차분이라고 부릅니다. 이렇게 개선한 수치미분을 파이썬으로 구현한 코드는 아래와 같습니다.
import numpy as np
import matplotlib.pylab as plt
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
def function_1(x):
return 0.01*x**2 + 0.1*x
def tangent_line(f, x):
d = numerical_diff(f, x)
print(d)
y = f(x) - d*x
return lambda t: d*t + y
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
tf = tangent_line(function_1, 5)
y2 = tf(x)
plt.plot(x, y)
plt.plot(x, y2)
plt.show()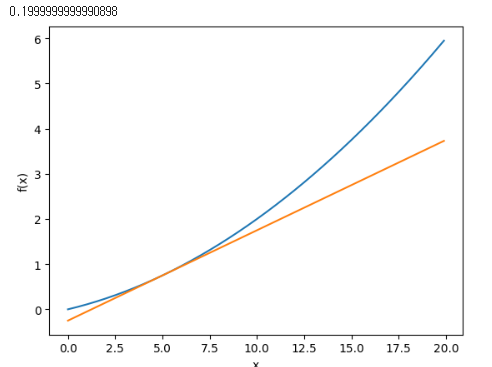
일변수 미분 $f'(x)$ 는 함수 $f$를 점 $x$에서 미분합니다.
$$ f'(x) = \lim_{h \to 0} \dfrac{f(x+h)-f(x)}{h} $$
다변수 방향 미분 $D_{\overrightarrow{v}} f(\mathbf{x}) $ 는 함수 $f$를 점 $\mathbf{x}$ 에서 미분합니다.
$$ D_{\overrightarrow{v}} f(\mathbf{x}) = \lim_{h \to 0} \dfrac{f(\mathbf{x} + h \overrightarrow{v}) - f(\mathbf{x})}{h} $$
다변수 함수의 미분은 일변수 함수의 미분과 비슷하게 정의되지만, 방향이 추가적으로 필요하게 됩니다. 따라서 이를 어떤 점에서 어떤 방향으로 미분하는지를 벡터를 통해 표현합니다.
간단한 다변수 함수를 미분해보면서 편미분과 그레디언트에 대해 확인해보겠습니다.
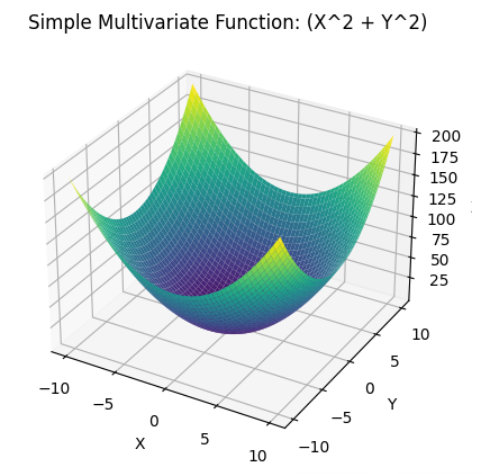
$$ f(x_0, x_1) = x_0^2+x_1^2 $$
이 간단해보이는 함수는 인수들의 제곱합을 더하는 함수이지만, 변수가 2개인 다변수 함수입니다. 따라서 이 함수는 3차원 그래프로 그려지는 함수입니다.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def simple_multivariate_function(x, y):
return x**2 + y**2
# 범위 설정
x_range = np.linspace(-10, 10, 100)
y_range = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x_range, y_range)
Z = simple_multivariate_function(X, Y)
# 3D 플롯 생성
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
# 축 레이블 설정
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# 제목 설정
plt.title('Simple Multivariate Function: (X^2 + Y^2)')
# 플롯 표시
plt.show()
이 때 이 함수 $f$ 를 미분할 때는 '어느 변수에 대한 미분이냐'를 구별해야 합니다. 즉 $x_0$에 대한 미분인지, $x_1$에 대한 미분인지를 구별해야한다는 것이고, 이처럼 변수가 여럿인 함수에 대한 미분을 편미분이라고 부릅니다. 정확한 정의는 아래 포스팅을 참고해주시면 되겠습니다.
다변수함수
정의역이 2개인 이변수 함수입니다. 즉 축이 정의역이 아닌 평면이 정의역이 되고, 그에 따른 함숫값? 높이...
blog.naver.com
모든 변수에 대해 편미분을 벡터로 정리한 것을 Gradient 라고 합니다. Gradient 는 물리적으로도 굉장히 중요한 의미를 가지게 되는데요, 바로 "최대 변화율" 을 나타내는 의미를 가지고 있습니다. 그레디언트는 정말 물리학적으로도 너무 중요한데, 딥러닝에서 그레디언트가 왜 중요한지를 결론부터 말하면 "함수의 출력 값을 가장 크게 줄이는 방향" 을 알려주기 때문입니다.
위 다변수 함수에 대한 그레디언트를 시각화해보면 아래와 같습니다.

지금 보면 그레디언트가 향하는 방향은 곧 위 함수의 최소점입니다. 이를 통해 추후 신경망의 학습에서 min 값을 찾는 방법에 사용하게 됩니다. 아래는 위 그림의 시각화 코드입니다.
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D
def _numerical_gradient_no_batch(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # x와 형상이 같은 배열을 생성
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h) 계산
x[idx] = float(tmp_val) + h
fxh1 = f(x)
# f(x-h) 계산
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 값 복원
return grad
def numerical_gradient(f, X):
if X.ndim == 1:
return _numerical_gradient_no_batch(f, X)
else:
grad = np.zeros_like(X)
for idx, x in enumerate(X):
grad[idx] = _numerical_gradient_no_batch(f, x)
return grad
def function_2(x):
if x.ndim == 1:
return np.sum(x**2)
else:
return np.sum(x**2, axis=1)
def tangent_line(f, x):
d = numerical_gradient(f, x)
print(d)
y = f(x) - d*x
return lambda t: d*t + y
if __name__ == '__main__':
x0 = np.arange(-2, 2.5, 0.25)
x1 = np.arange(-2, 2.5, 0.25)
X, Y = np.meshgrid(x0, x1)
X = X.flatten()
Y = Y.flatten()
grad = numerical_gradient(function_2, np.array([X, Y]) )
plt.figure()
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy",color="#666666")#,headwidth=10,scale=40,color="#444444")
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.xlabel('x0')
plt.ylabel('x1')
plt.grid()
plt.draw()
plt.show()
추가적으로 다른 분야에서 그레디언트가 무슨 의미를 가지는지에 대해 예전에 포스팅했던 내용입니다. 관심 있으신 분들은 한 번 보시라고 링크 걸어놓고 가겠습니다.
Gradient(그레디언트)
오늘은 Gradient가 무엇인가 알아보도록 하겠습니다. 관련 연산인 divergence 와 curl의 개념도 살짝 맛보...
blog.naver.com

Reference :
밑바닥부터 시작하는 딥러닝 (저자 : 사이토 고키 / 번역 : 이복연 / 출판사 : 한빛미디어)
'딥러닝(DL) > 딥러닝 기초' 카테고리의 다른 글
| [DL] 학습 알고리즘 구현 ( 2층 신경망 ) (0) | 2023.08.18 |
|---|---|
| [DL] 경사 하강법 ( Gradient Descent ) (0) | 2023.08.17 |
| [DL] 정보 엔트로피 ( Information Entropy ) (0) | 2023.08.07 |
| [DL] 손실 함수 ( Loss function ) (0) | 2023.08.03 |
| [DL] MNIST ( Modified National Institute of Standards and Technology database ) (0) | 2023.07.31 |