정보이론은 최대한 많은 데이터를 매체에 저장하거나 채널을 통해 통신하기 위해 데이터를 정량화하는 수학의 한 분야입니다. 쉬운 말로 정보량을 수치화 할 수 있을까? 라는 질문에서 시작된 것이 정보이론입니다. 정보 엔트로피란 정보 이론에서 나타난 개념으로, 보통 엔트로피라는 단어는 화학이나 물리에서, 열역학에 대해 배울 때 가장 먼저 듣게 될텐데 실제로 정보 엔트로피는 섀넌이 열역학에서 정의된 엔트로피를 확장한 개념으로 열역학에서의 엔트로피와 크게 다르지 않은 개념입니다.
딥러닝을 하는데 갑자기 무슨 열역학? 엔트로피? 라고 생각할 수 있지만 지난 포스팅에서 소개했듯 손실 함수로 자주 사용되는 크로스 엔트로피라는 것도 배웠고, 이를 이해하기 위해서는 엔트로피에 대해 자세히 알 필요가 있습니다. 또한 자연어 처리나 논문 등 다른 분야에서도 정보이론에 대한 기초 개념이 나타나는 경우가 정말 많기 때문에 딥러닝에 필요한 정보 이론의 기초 개념, 그 중에서도 엔트로피에 대해 알아보는 포스팅입니다.
엔트로피(Entropy) 란?
$$ p(x) = \text{Pr} \{X=x\}, \quad x \in \chi $$
$X$가 discrete random variable, 즉 이산 확률 변수로 정의될 때 $X$에 대한 확률 질량 함수(Probability mass function) 은 $p(x)$ 처럼 정의할 수 있습니다. 위처럼 정의된 이산 확률 변수 $X$에 대해 엔트로피 $H(x)$를 정의합니다.
$$ H(X) = - \sum_{x \in \chi} p(x) \log p(x) $$
위 정의에서 $\text{log}$의 밑수는 따로 명시되어 있지 않으면 2로 생각하면 되고, 정보이론에서는 $0\text{log}0 = 0$ 으로 정의합니다. 이는 마치 신호와 시스템에서 단위 계단 함수의 $x=0$에서의 함숫값이 $\dfrac{1}{2}$이다 라고 정의하는 것과 비슷한 맥락입니다. 수학적으로 엄밀하지는 않더라도 "앞으로 그렇게 사용하겠다" 라고 하는 것이죠. 실제로 $\text{log}_0$은 정의되지 않지만 정보이론에서는 $0\text{log}0 = 0$ 으로 정의합니다.
즉 엔트로피는 확률 변수가 만들어내는 확률 분포에 의해 정의됩니다.
위 정의가 어려워보이지만 일반화된 식이라 그렇게 보이는 것이고 실제로 의미는 직관적이고 간단합니다. 만약 동전을 던지는 사건 $X$에 대해 앞면이 나올 확률이 $p$, 뒷면이 나올 확률이 $1-p$라고 해봅시다. 동전을 던지면 무조건 앞면이나 뒷면이 나올 수 밖에 없기 때문에 이 두 확률의 합은 당연히 $1$이 되어야 합니다.
$$ X=\begin{cases}1\quad \ \ \ \ \ \ \ \ \ \ \text{with probability }p\\0\quad \quad \ \ \ \ \ \ \text{with probability }1-p\end{cases} $$
동전 던지기 사건 $X$를 수식으로 나타내면 위와 같습니다. $1$이라는 사건이 앞면, $0$이라는 사건이 뒷면이라고 생각하면 됩니다. 위의 확률 분포에 대한 엔트로피를 나타내면 아래와 같이 간단하게 나옵니다. 확률과 $\text{log}$확률을 곱하고 마이너스 부호를 붙여서 더하면 끝입니다.
$$ H(X) = -p\text{log}p - (1-p)\text{log}(1-p) $$
만약 동전 던지기에서 앞면이 나올 확률과 뒷면이 나올 확률이 같다고 가정하면, 즉 $p= 1/2$ 라고 생각하면 엔트로피의 계산 결과는 $H(X) = - 0.5 \text{log}_2(0.5) - 0.5\text{log}_2(0.5) = 0.5+0.5 = 1$ 이 나옵니다. 만약 극단적으로 동전 던지기에서 10번을 던졌는데 모두 앞면만 나왔거나 모두 뒷면만 나온 경우, 즉 $p = 0 \text{ or } p = 1$ 인 경우 엔트로피를 계산해보면 $H(X) = 0$ 이 나오게 됩니다.
그러면 도대체 이런 엔트로피를 왜 정의하고 계산하는가를 알아야겠죠? 여기서 배울 엔트로피의 가장 중요한 특징은 엔트로피는 정보의 불확실성의 정도를 측정합니다(Entropy measures the uncertainty.). 아직 감이 잘 안올테니 쉬운 예시인 위의 동전 던지기의 엔트로피를 계속 살펴보겠습니다. 동전 던지기에 대한 엔트로피 그래프를 그려보면 아래와 같습니다.
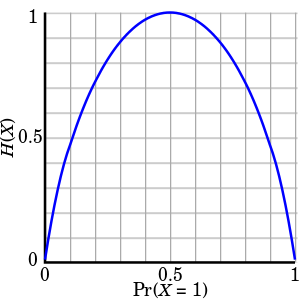
우리가 동전 던지기를 하는데 불확실성이 클 때는 언제일까요? 앞면과 뒷면이 각각 나올 확률이 동일한 $p=1/2$일 때보다 앞면이나 뒷면만 계속 나오는 상황이 훨씬 불확실성이 작습니다. 좀 헷갈릴 수 있는데 10번 던지면 무조건 앞면만 나오게 떨어지는 특수 동전이 있고, 진짜 반반 확률로 나오는 동전이 있는데 이 두 개의 동전으로 동전 던지기를 할 경우 불확실성이 작은 것은 당연히 특수 동전이겠죠? 무조건 앞면이나 뒷면이 나오게 되면 불확실성이 없으므로 엔트로피 또한 $0$입니다. 이는 위 그래프의 $0$과 $1$에서의 $H(X)$가 $0$인 것으로 쉽게 확인할 수 있습니다. 그렇다면 동전 던지기에서 불확실성이 가장 큰 것은 앞면과 뒷면이 동일한 확률로 나타날 때이고, 이는 곧 엔트로피가 가장 큰 지점이라는 것을 알 수 있습니다.
그리고 이러한 엔트로피가 등장한 배경은 "정보(불확실성)를 수치화할 수 있는가, 얼마나 효율적으로 정보를 저장할 수 있는가?" 였습니다. 따라서 엔트로피의 범위 또한 엔트로피의 중요한 특징 중 하나인데, 엔트로피는 $\text{log}$(사건의 개수) 보다 무조건 작거나 같다는 것이 수학적으로 증명되어 있습니다.
$$ H(X) ≤ \text{log} | \chi | $$
또한 엔트로피와 $\text{log}$(사건의 개수) 가 같아지는 시점은 $X$가 $\chi$ 전체에 대해 uniform distribution, 즉 균등 분포일 경우에 $H(X) = \text{log}|\chi|$ 가 성립합니다. 위 동전 던지기의 예로는 $p=1/2$일 때 엔트로피가 가장 커지고, $\text{log}_2 2$ 가 되는 것입니다. 기본적으로 밑은 2이고, 사건의 개수가 2개밖에 없으므로 동전 던지기 사건의 엔트로피는 $1$보다 커질 수 없는 것이죠.
만약 주사위 던지기를 생각해본다면 주사위는 1,2,3,4,5,6 이라는 6개의 경우가 나타날 수 있습니다. 이 때 만약 주사위의 각 눈이 나오는 확률이 $1/6$으로 동일하다면 주사위 던지기 사건에서 나타날 수 있는 엔트로피의 최댓값은 계산하지 않아도 $\text{log}_2 6$ 이 됩니다.
또한 다른 해석으로 엔트로피를 이해할 수도 있습니다. 그러려면 우선 섀넌이 정의한 "정보량" 이 무엇인지를 알아야 합니다. 섀넌은 $-log \{p(x_i)\}$ 의 형태로 정보량을 정의합니다. 이 때 $x_i$는 사건들을 말합니다. 위의 주사위 던지기 같은 예에서 1,2,3,4,5,6 을 말하는 것이죠. $p(x_i)$는 사건이 발생할 확률을 뜻합니다. 즉, 확률에 $\text{log}$를 씌운 그 값을 정보량이라고 정의하고 사용합니다. 이 때 위에서는 밑이 $2$인 정보량만 확인했었는데 밑이 $2$인 경우 정보량의 단위는 $bit$ 이 되며, 밑이 자연상수 $e$인 경우 단위는 $nat$ 이 됩니다.
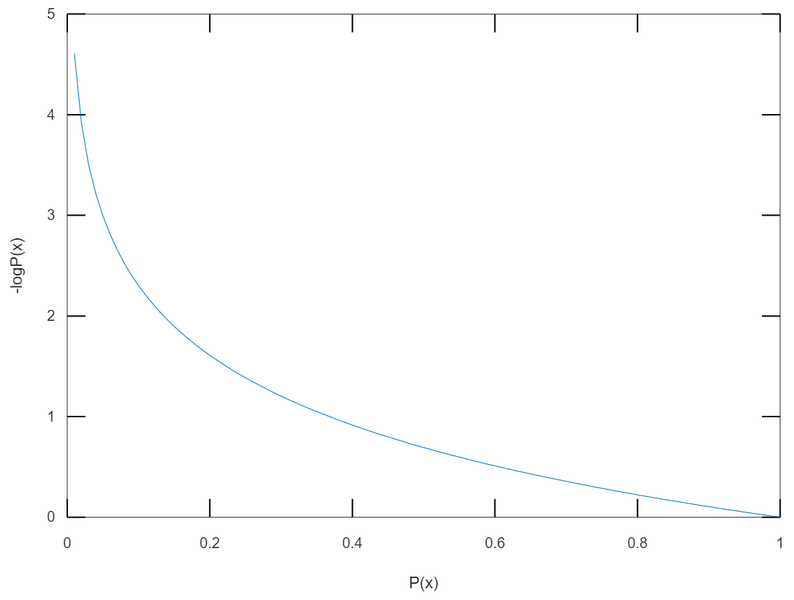
즉 어떤 사건의 발생 확률 $p(x_i)$ 가 낮을수록 정보량은 크고, 높을수록 정보량은 작습니다. $\text{log}$의 밑이 1보다 큰 경우는 $-\log$ 함수는 위처럼 단조 감소함수가 되기 때문에 확률이 1에 가까워질수록 정보량은 0으로, 확률이 0에 가까울수록 정보량은 무한대에 가까워집니다.
뭔가 직관이랑 와닿지가 않는 내용입니다. 확률이 높으면 정보량이 높아야 하지 않나? 그런데 왜 섀넌이 이렇게 정의했는지를 알면 이해가 갑니다.
"섀넌은 어떤 사건이 지니고 있는 정보량을 그 사건의 발생 확률로 정의했다. 매일 맑기만 한 곳에서 맑은 날씨라는 것은 그 어떤 정보도 지니지 않는다. 날씨는 맑은 것이 당연하기 때문에. 하지만 아주 가끔 비가 온다면 그건 아주 놀라운 일일 것이다. 마치 아프리카에 내리는 눈처럼"
정보량에 대한 개념을 숙지했으면 아까 확인했던 엔트로피를 새로운 시각으로 이해할 수 있습니다. 바로 "전체 상태에 대한 정보량의 기대치(평균)" 으로 해석할 수 있습니다.
$$ H(X) = - \sum_{x \in \chi} p(x) \log p(x) = \mathbb{E} \left( \log \dfrac{1}{p(x)} \right)$$
$\log(1/p(x))$는 사건 $x$가 일어 난 경우 얻는 정보량으로 해석할 수 있습니다. 이렇게 해석하면 $H(X)$는 모든 사건에 대한 정보량의 기댓값인 평균 정보량이 됩니다.
상호 정보량(Multual Information) / 조건부 엔트로피(Conditional Entropy)
상호 정보량의 엄밀한 정의는 결합확률밀도함수 $p(x,y)$와 주변확률밀도 함수의 곱 $p(x)p(y)$의 KL divergence 입니다. KL divergence 라는 개념은 포스팅의 맨 아래에서 다룹니다. 상호 정보량이란 결국 결합확률밀도함수와 주변확률밀도함수의 차이를 측정함으로써 두 확률 변수의 상관관계를 측정하는 방법을 말합니다. 혹은 하나의 확률변수가 다른 하나의 확률변수에 대해 제공하는 정보의 양을 의미합니다.
$$ \begin{align*} I(X;Y) &= \sum_{x \in \chi} \sum_{y \in \phi} p(x, y) \log \dfrac{p(x, y)}{p(x)p(y)} \\ &= \sum_{x \in \chi} \sum_{y \in \phi}p(x,y)\log p(x,y) - \sum_{x \in \chi} \sum_{y \in \phi} p(x,y) \log p(x) - \sum_{x \in \chi} \sum_{y \in \phi} p(x,y) \log p(y) \\ &= -H(X, Y) + H(X) + H(Y) \\ &= H(X) - H(X|Y) \\ &= H(Y) - H(Y|X) \\ &= I(Y;X) \end{align*}$$
만약 두 확률변수가 독립이라면 상호정보량은 0이 되고, 반대로 상관관계가 있다면 그만큼의 상호정보량을 가지게 됩니다. 전개에서 볼 수 있듯 $X$가 $Y$에 대해 제공하는 정보량과 $Y$가 $X$에 대해 제공하는 정보량은 같습니다. 따라서 상호 정보량은 두 확률변수가 공유하는 엔트로피 라고 해석할 수도 있습니다.
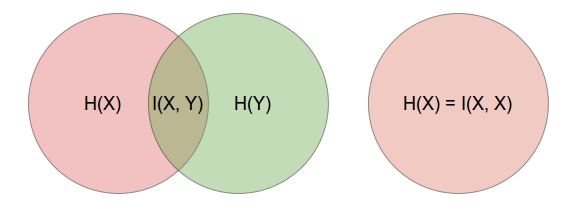
조건부 엔트로피(Conditional Entropy)란 다음 수식대로 정의됩니다.
$$ \begin{align*} H(Y|X) &= \sum _{x\in \chi }^{\ }p(x)H(Y|X= x) \\ &= -\sum_{x \in \chi} p(x) \sum_{y \in \phi}p(y|x) \text{log}p(y|x) \\ &= - \sum_{x \in \chi} \sum_{y \in \psi} p(x,y) \text{log}p(y|x) \end{align*} $$
즉 조건부 엔트로피란 확률변수 $Y$의 값이 관측되었을 때, 확률 변수 $X$가 발생할 확률에 대한 정보량의 기댓값 입니다. 조건부 확률을 안다면 매우 쉬운 개념입니다. $y$라는 사건이 발생했을 때 $x$라는 사건이 발생할 확률을 정보량 $-\log p(x, y)$ 로 나타내고, 사건 $y$를 전제로 한 기댓값을 구합니다. 그리고 전체 $y$에 대한 기댓값을 구합니다. 위 수식은 복잡해보이지만 잘 살펴보면 위에 말한대로 $-\log p(y|x)$ 의 기댓값이라고 해석할 수 있습니다
이 때 조건부 확률 $P(X|Y) ≠ P(Y|X)$ 일 수 있기 때문에 (같은 경우도 존재) 보통 $H(Y|X) ≠ H(X|Y)$ 인 관계가 나타납니다. 같을 수 없다는 아니지만 같다는 보장이 없고 굉장히 특수한 형태에서만 같게 나오며 일반적으로 다른 값이 나오게 됩니다.
또한 이렇게 다른 확률변수를 결합하는 것을 Conditioning 이라고 하는데, 이러한 Conditioning은 엔트로피를 줄여줍니다.(독립이 아닌 경우) 따라서 아래와 같은 관계가 성립합니다.
$$ H(X|Y) ≤ H(X) $$
엔트로피는 계산해보면 결합 분포의 엔트로피가 더 작거나 같게 나타납니다. 이는 직관적으로도 이해할 수 있는데요, 엔트로피는 불확실성을 나타내므로 어떤 확률변수 $X$가 있는데 추가적인 가정을 한다면? 당연히 불확실성은 더 줄어들게 될 것입니다.
만약 두 사건이 독립인 경우, 두 사건이 전혀 상관없는 경우에는 결합을 하더라도 엔트로피가 줄어들지 않습니다. 만약 내일 날씨가 비가 올지, 맑을지에 대한 확률 분포에 내가 방금 동전을 던져서 앞면이 나왔다면? 이라는 가정을 추가한다하더라도 내일 날씨에는 전혀 영향을 끼치지 않습니다. 그 말은 곧 원래의 엔트로피에도 전혀 영향을 미치지 않는다는 것이죠.
또한 이 개념을 확장하면 $H(X|Y) = 0$의 의미를 해석할 수 있습니다.
결합 확률분포에 대한 엔트로피가 0이라는 말은 곧 $Y$라고 가정하면 $X$에 대한 불확실성이 0이 된다는 것을 의미합니다. 이 말은 곧 $X$가 일어날 사건이 모두 $Y$에 포함되어 있고, 다른 말로 $X$가 $Y$의 함수라는 말입니다.
아주 쉬운 예시를 들어봅시다. $X$는 주사위를 던져서 나오는 확률 분포라고 해보고, $Y$는 결과가 홀수 or 짝수인 확률 분포입니다. 주사위를 던져봤자 무조건 짝수나 홀수가 나오게 되겠죠? 주사위를 던지기 이전에 이 결과는 홀수이거나 짝수일 것이다. 라는 가정을 하고 엔트로피를 구하면 무조건 이 가정에 부합하기 때문에 결합 엔트로피가 0이라는 말이 됩니다. 이를 다른 용어로 deterministic, 결정론 적이다, 결정되었다 라고 표현합니다.
즉 조건부 엔트로피가 0인 경우는 오직 deterministic 한 경우밖에 없습니다.
또한 조건부 엔트로피를 사용하면 상호 정보량을 새롭게 전개할 수 있습니다.
$$ \begin{align*} I(X;Y) &= \sum_{x \in \chi} \sum_{y \in \phi} p(x, y) \log \dfrac{p(x, y)}{p(x)p(y)} \\ &= \sum_{x \in \chi} \sum_{y \in \phi}p(x,y)\log \dfrac{p(x,y)}{p(y)} - \sum_{x \in \chi} \sum_{y \in \phi} p(x,y) \log p(x) \\ &= \sum_{x \in \chi} \sum_{y \in \phi}p(y)(p(x|y)\log \{p(x|y) \} - \sum_{x \in \chi} \log \{ p(x)\} \sum_{y \in \phi} p(x, y) \\ &= - \left[ - \sum_{x \in \chi} \sum_{y \in \phi} p(y)p(x|y) \log \{p(x|y) \} \right] + \left [ - \sum_{x \in \chi} p(x) \log\{p(x)\} \right] \\ &= -H(X|Y) + H(X) \end{align*}$$
위 수식에서 주목해서 봐야할 부분은 $H(X) - H(X|Y)$입니다. 위 전개에는 쓰지 않았지만 $H(Y)-H(Y|X)$도 동일한 값을 가집니다. 이제 우리가 조건부 엔트로피의 개념을 알았으므로 이 식의 개념까지 해석할 수 있습니다. $H(X|Y)$는 무조건 $H(X)$ 보다 클 수는 없으며, $H(X)$ 란 $X$에 대한 불확실성을 의미하고, $H(X|Y)$는 $Y$를 알았을 경우의 $X$의 불확실성을 의미합니다. $H(X|Y)$를 뺀다는 것은 정보량이 줄어드는 것을 의미하는데 왜 줄어들었을까요? $Y$를 알았기 때문에 줄어들었을텐데 $Y$가 $X$에 대한 정보를 가지고 있고, 그 정보를 우리가 알았기 때문에 불확실성이 줄어든다 라고 해석할 수 있습니다. 그러면 불확실성이 얼마만큼 줄어들었는가? 는 확률변수 $Y$가 확률변수 $X$에 대해 가지고 있는 정보량 만큼 불확실성이 줄었다고 해석이 가능합니다. 줄어든 불확실성의 양, 줄어든 엔트로피의 양이 확률변수 $Y$가 확률변수 $X$에 대해 가지고 있는 정보의 양 이 되는 것입니다. 즉, 지금까지 이렇게 어려운 수식을 나타냈던 것은 정보를 정량화 하기 위함이었던 것이죠.
$$ I(X;Y) ≥ 0 $$
따라서 상호 정보량은 항상 0보다 크다는 성질을 가지고 있습니다. 또한 상호정보량이 0이 되기 위한 필요충분조건은 $X$와 $Y$가 독립 이라는 것입니다.
지금까지는 엔트로피가 불확실성의 정도를 나타내는 어떤 양이고, 정보를 정량화하기 위한 개념인 상호 정보량과 조건부 엔트로피의 개념에 대해 알아보았습니다. 위에서 주황색으로 표시한 것들이 엔트로피의 제가 생각하는 중요한 개념들입니다. 엔트로피는 정말 중요한 특징이 더 있는데요, 바로 어떤 정보를 표현하고 압축하려고 할 때(최소한의 크기로 정보를 나타내고 싶을 때) 최소한의 크기가 있는데 그 최소한의 크기에 대한 것을 알려준다는 사실입니다. Entropy is the fundamental limit for the compression of information. (영어가 의미 그대로를 전하는 것 같아 그대로 적습니다). 즉 엔트로피, 그리고 위에서 배운 상호 정보량은 정보의 압축과 전달을 수치화하는 중요한 개념이 됩니다.
$$ L(C) = \sum_{x \in \chi} p(x)l(x) $$
우리가 어떤 정보를 송수신할 때는 모두 이진 코드로 바꿔서 보냅니다. 컴퓨터가 처리하는 방식이 2진수이기 때문이죠. 따라서 이진코드의 길이를 줄이는 것이 곧 정보의 압축과 동일합니다. 코드의 길이를 $l(x)$ 라고 나타내고 그리고 $p(x)$는 확률 질량 함수입니다. 쉽게 생각해보면 빈도수? 를 나타내는, 문장에서 이 단어가 등장할 확률 같은 것을 의미합니다. $L(C)$가 의미하는 것은 즉 코드의 길이의 기댓값이 됩니다. 정보를 잘 압축시킨다는 것은 곧 $L(C)$를 최소화 시키는 것을 의미합니다. 정보를 압축하는 대표적인 예시로 허프만 코드 같은 것들이 있습니다.
허프만 코드란 알파벳이 등장하는 비율을 통해 자주 등장하는 알파벳을 가장 짧은 형태의 코드와 대응 시키고, 자주 등장하지 않는 알파벳을 긴 코드와 대응시켜 영문 텍스트의 저장 크기를 줄이는 알고리즘입니다. 허프만 코드에 대한 자세한 내용은 다른 링크를 달도록 하겠습니다.
Huffman coding - Wikipedia
From Wikipedia, the free encyclopedia Technique to compress data Huffman tree generated from the exact frequencies of the text "this is an example of a huffman tree". Encoding the sentence with this code requires 135 (or 147) bits, as opposed to 288 (or 18
en.wikipedia.org
우리가 단어를 코드로 바꿔서 전송을 할 때 전송 데이터를 계속해서 작게 압축시키고 싶지만 더 작게 만들 수 없는 최소한의 한계 지점이 있습니다. 그리고 그 한계 지점은 Shannon's source coding theorem 에 증명되어 있는데요, 그 정보 압축의 최소 한계 지점이 곧 엔트로피 입니다.
$$ L ≥ H(X) $$
또한 이론적으로 최대한 이상적인 코드까지 압축을 시킨다면 다음 범위에 존재한다는 것이 이론적으로 증명되어 있습니다.
$$ H(X) ≤ L^* ≤ H(X) + 1 $$
$L^*$는 optimal code의 길이 기댓값을 의미합니다. 반대로 말하면 엔트로피를 계산함으로써 최대한 줄일 수 있는 가장 효율적인 코드의 범위를 알아낼 수 있습니다.
쿨백-라이블러 발산 / 상대 엔트로피 (KL divergence / Relative entropy)
마지막으로 엔트로피의 의미 중 머신 러닝에서 가장 많이 사용되는 개념이 있습니다. 크로스 엔트로피에서도 사용되었던 개념입니다. 상대 엔트로피는 두 확률 분포 간의 거리(관계)를 나타낼 때 사용할 수 있습니다. KL divergence(Kullback-Leibler divergence) 와 상대 엔트로피는 같은 말입니다. 다른 이름으로는 정보 획득량(Information gain), 정보 발산(Information divergence)로 부르기도 합니다. 이는 위에서 말한대로 두 확률분포가 얼마나 비슷한 분포인지 둘의 차이를 계산하는데 사용하는 함수 를 의미합니다.
$$ D_{KL}(p||q) = \sum_{x \in \chi} p(x) \log \dfrac{p(x)}{q(x)} $$
$$ D_{KL}(p||q) ≥ 0 $$
두 확률분포 사이의 "거리"를 측정하기 때문에 KLD는 항상 0보다 크거나 같습니다. 그러나 수학적으로 KLD는 거리 함수가 아닙니다. 단적인 예로 두 점의 위치가 서로 바뀐다고 해도 거리는 변하지 않지만, KLD의 경우는 두 값의 위치를 바꾸면 함수값도 달라집니다. 직관적인 이해를 위해 거리 라는 용어를 사용합니다. KLD가 $0$인 경우는 두 확률분포 사이의 거리라고 이해하면 당연히 두 확률변수가 같은 경우 KLD의 계산 결과가 $0$이 나오게 될 것입니다.
마지막으로 요약 겸 가장 중요한 일반화를 해보도록 하겠습니다. 위에서 배웠던 개념들은 따로따로 알아야 하는 개념이 아니라 모두 연관이 되어 있는 개념들로 지금 내용을 쓰기 위해 배운 내용들입니다.
엔트로피는 불확실성을 측정하는 양으로, 확률분포에 의해 정의되며 이는 곧 전체 정보량의 기댓값으로 생각할 수 있었습니다. 또한 엔트로피는 정보 압축의 최소 한계를 가리키는 의미를 가지기도 했습니다. 그 다음으로 상호 정보량이라는 것을 배웠는데, 하나의 확률변수가 다른 하나의 확률변수에 대해 제공하는 정보의 양을 의미하며 불확실성이 얼마만큼 줄어들었는가? 를 계산함으로써 하나의 확률변수가 다른 하나의 확률변수에 대해 가지고 있는 정보의 양을 의미한다는 것을 배웠습니다.
$$ I(X;X) = H(X) $$
두 개의 확률변수에 대해서 상호 정보량에 대해 배우기 시작했지만, 엔트로피는 동일한 확률 변수에 대한 상호 정보량으로 일반화 될 수 있습니다. 상호정보량은 $I(X;X) = H(X) - H(X|X)$ 로 구할 수 있는데 뒤에 빼는 항의 의미를 생각해보면 $X$를 알았을 때의 $X$의 엔트로피입니다. $X$를 아는 상태에서는 당연히 불확실성이 $0$이 되기 때문에 상호 정보량은 엔트로피의 일반화된 표현이기도 합니다.
마지막으로 두 확률분포 간의 유사성, 거리를 나타내는데 사용하는 상대 엔트로피, KL divergence 에 대해 배웠습니다. 상호 정보량이 엔트로피의 일반화였던 것처럼, 상대 엔트로피를 사용해 상호 정보량을 일반화 할 수 있습니다.
$$D_{KL} (p(x,y)||p(x)p(y)) = \sum_{x \in \chi} \sum_{y_ \in \phi} p(x,y) \log \dfrac{p(x,y)}{p(x)p(y)} = I(X;Y)$$
두 개의 확률 분포에 대해 상대 엔트로피를 구하면 그 값이 곧 상호 정보량이 나오게 됩니다. 만약 2개의 확률 변수가 독립이라면 $p(x,y) = p(x)p(y) $라는 식이 성립합니다. 그렇게 되면 위 식은 같은 확률 변수에 대해 상대 엔트로피를 구하는 것이기 때문에 당연히 $0$이 나와야 합니다. 즉 $p(x,y)$ 랑 $p(x)p(y)$ 의 차이가 커질수록 상대 엔트로피가 더 크게 나오게 될것이고, 더 많이 종속되었다고 생각할 수 있습니다.
다음으로 지난 포스팅에서 배웠던 크로스 엔트로피(Cross entropy)에 대해서도 배워보겠습니다. 지난 번에 무슨 의미인지 알 수 없던 수식들이 오늘 포스팅을 천천히 읽어보셨으면 이젠 이해가 되실 겁니다.
$$ H(p, q) = - \sum_{x \in \chi}p(x) \log q(x) $$
크로스 엔트로피는 확률 변수가 2개가 주어졌을 때 2개의 확률 질량 함수 $p(x)$, $q(x)$에 대하여 위 수식대로 정의됩니다. 처음 봤을 때는 뭐하는 식인가 싶었겠지만 지금은 되게 익숙한 모양의 식입니다. 오늘 배운 상대 엔트로피와 크로스 엔트로피와 엔트로피 사이에는 아래와 같은 관계식이 성립합니다.
$$ \begin{align*} D(p||q) &= \sum_{x \in \chi }p(x) \log \dfrac{p(x)}{q(x)} \\ &= - \sum_{x \in \chi} p(x) \log q(x) + \sum_{x \in \chi} p(x) \log p(x) \\ &= H(p, q) - H(p) \end{align*} $$
2번째 줄의 왼쪽 정의는 크로스 엔트로피의 정의이고 오른쪽은 엔트로피의 정의( - 부호를 붙이면) 입니다. 즉 상대 엔트로피는 크로스 엔트로피 - 엔트로피 라는 관계를 가지고 있으며 지금까지 설명해왔던 모든 의미들이 크로스 엔트로피에도 그대로 적용된다는 것입니다.
일반적으로 머신러닝에서는 $p$를 상수로 놓고(정답 레이블) $q$를 학습을 통해 예측한 추정치로 사용합니다. 머신러닝의 성능이 좋아진다는 것은 $q$를 계속해서 $p$로 근사시키는 작업이 됩니다. 둘 사이의 차이를 의미하는 상대 엔트로피가 줄어들어야 예측과 정답의 차이가 줄어든다는 것인데, $p$가 상수라면 $H(p)$ 또한 변하지 않기 때문에 $D(p||q)$를 줄인다는 것은 곧 크로스 엔트로피 $H(p, q)$를 줄인다는 것과 같습니다. 머신 러닝의 입장에서 상대 엔트로피와 크로스 엔트로피는 큰 차이가 없는 것이죠(상수 차이만 남, 실제 머신러닝에서 $p$를 one-hot vector 로 잡게 되면 $H(p)$까지 $0$이 된다).
즉 머신러닝이란 정답과 예측치의 차이를 줄이는 것이고, 데이터를 벡터로 표현하기 때문에 2개의 벡터간의 크로스 엔트로피를 줄이는 작업이라고 생각할 수 있고, 그렇기 때문에 우리가 손실함수로 크로스 엔트로피 함수를 많이 사용하는 것입니다.

Reference :
Elements of Information Theory - Cover, Tomas
http://www.scholarpedia.org/article/Mutual_information
https://en.wikipedia.org/wiki/Mutual_information
https://en.wikipedia.org/wiki/Entropy_(information_theory)
https://horizon.kias.re.kr/18474/
https://hyunw.kim/blog/2017/10/27/KL_divergence.html
https://arxiv.org/abs/1304.2333
https://en.wikipedia.org/wiki/Shannon%27s_source_coding_theorem
'딥러닝(DL) > 딥러닝 기초' 카테고리의 다른 글
| [DL] 경사 하강법 ( Gradient Descent ) (0) | 2023.08.17 |
|---|---|
| [DL] 수치 미분 ( Numerical differentiation ) (0) | 2023.08.11 |
| [DL] 손실 함수 ( Loss function ) (0) | 2023.08.03 |
| [DL] MNIST ( Modified National Institute of Standards and Technology database ) (0) | 2023.07.31 |
| [DL] 인공 신경망 ( Artificial neural network, ANN ) - Forward Propagation (0) | 2023.07.27 |